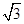题目内容
棱长为1的正方形ABCD-A1B1C1D1的8个顶点都在球O的表面上,则球O的表面积是 ________;设E、F分别是该正方形的棱AA1、DD1的中点,则直线EF被球O截得的线段长为 ________.
3π 
分析:由题意可知正方体的体对角线计算球的直径,求出对角线的长可得球的直径,求出半径,即可求出球的表面积;如图所示,OP 是球的半径,OQ是棱长的一半,求出PQ的2倍即可求出直线EF被球O截得的线段长.
解答: 解:正方体对角线为球直径,A1A2=3,
解:正方体对角线为球直径,A1A2=3,
所以 ,所以球的表面积为3π;
,所以球的表面积为3π;
由已知所求EF是正方体在球中其中一个截面的直径,
d= ,所以
,所以 ,
,
所以2PQ=2r= .
.
故答案为:3π;
点评:本题考查正方体的外接球,球的表面积的计算,球的截面知识,考查计算能力,空间想象能力,正确利用条件求解直线EF被球O截得的线段长,是本题的难点,结合图形直观,易于解题.

分析:由题意可知正方体的体对角线计算球的直径,求出对角线的长可得球的直径,求出半径,即可求出球的表面积;如图所示,OP 是球的半径,OQ是棱长的一半,求出PQ的2倍即可求出直线EF被球O截得的线段长.
解答:
 解:正方体对角线为球直径,A1A2=3,
解:正方体对角线为球直径,A1A2=3,所以
 ,所以球的表面积为3π;
,所以球的表面积为3π;由已知所求EF是正方体在球中其中一个截面的直径,
d=
 ,所以
,所以 ,
,所以2PQ=2r=
 .
.故答案为:3π;

点评:本题考查正方体的外接球,球的表面积的计算,球的截面知识,考查计算能力,空间想象能力,正确利用条件求解直线EF被球O截得的线段长,是本题的难点,结合图形直观,易于解题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在棱长为1的正方体ABCD-A1B1C1D1中,O为正方形ABCD的中心,E、F分别为AB、BC的中点,则异面直线C1O与EF的距离为
如图,在棱长为1的正方体ABCD-A1B1C1D1中,O为正方形ABCD的中心,E、F分别为AB、BC的中点,则异面直线C1O与EF的距离为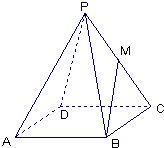 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,侧棱PA的长为2,且PA与AB、AD的夹角都等于60°,M是PC的中点,设
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,侧棱PA的长为2,且PA与AB、AD的夹角都等于60°,M是PC的中点,设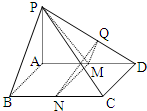 已知四棱锥P-ABCD,底面是边长为1的正方形,侧棱PA⊥底面ABCD且PA=1,M、N分别为AD、BC的中点,MQ⊥PD于Q.
已知四棱锥P-ABCD,底面是边长为1的正方形,侧棱PA⊥底面ABCD且PA=1,M、N分别为AD、BC的中点,MQ⊥PD于Q.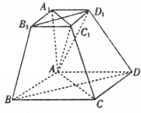 (2012•安徽模拟)如图,已知四棱台ABCD-A1B1C1D1的侧棱A1A垂直于底面AB-CD,底面ABCD是边长为2的正方形,四边形A1B1C1D1是边长为1的正方形,DD1=2.
(2012•安徽模拟)如图,已知四棱台ABCD-A1B1C1D1的侧棱A1A垂直于底面AB-CD,底面ABCD是边长为2的正方形,四边形A1B1C1D1是边长为1的正方形,DD1=2. B.
B.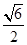 C.
C.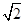 D.
D.