题目内容
3. 如图所示,阴影部分表示的角的集合为(含边界){α|kπ≤α≤kπ+$\frac{π}{3}$,k∈Z}(用弧度表示).
如图所示,阴影部分表示的角的集合为(含边界){α|kπ≤α≤kπ+$\frac{π}{3}$,k∈Z}(用弧度表示).
分析 阴影部分表示的角α位于一、三象限,在第一象限,0≤α≤$\frac{π}{3}$;在第三象限,π≤α≤$\frac{4π}{3}$,由此能求出阴影部分表示的角的集合(含边界).
解答  解:如图,阴影部分表示的角α位于一、三象限,
解:如图,阴影部分表示的角α位于一、三象限,
在第一象限,0≤α≤$\frac{π}{3}$;在第三象限,π≤α≤$\frac{4π}{3}$,
∴阴影部分表示的角的集合为(含边界):
{α|2kπ≤α≤2kπ+$\frac{π}{3}$或(2k+1)π≤α≤(2k+1)π+$\frac{π}{3}$,k∈Z}={α|kπ≤α≤kπ+$\frac{π}{3}$,k∈Z}.
故答案为:{α|kπ≤α≤kπ+$\frac{π}{3}$,k∈Z}.
点评 本题表示角的集合的求法,是基础题,解题时要认真审题,注意终边相同的角的集合的合理运用.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
14.数列{an}共有六项,其中四项是1,其余两项各不相同,则满足上述条件的数列{an}共有( )
| A. | 30个 | B. | 31个 | C. | 60个 | D. | 61个 |
8.如果α是第三象限角,则-$\frac{α}{2}$是( )
| A. | 第一象限角 | B. | 第一或第二象限角 | ||
| C. | 第一或第三象限角 | D. | 第二或第四象限角 |
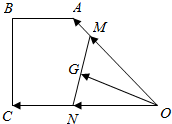 如图所示,已知直角梯形ABCO中,∠ABC=∠BCO=90°,AB=1,BC=$\sqrt{3}$,OA=OC=2,设$\overrightarrow{OM}$=m$\overrightarrow{OA}$,$\overrightarrow{ON}$=n$\overrightarrow{OC}$(其中0<m,n<1),G为线段MN的中点.
如图所示,已知直角梯形ABCO中,∠ABC=∠BCO=90°,AB=1,BC=$\sqrt{3}$,OA=OC=2,设$\overrightarrow{OM}$=m$\overrightarrow{OA}$,$\overrightarrow{ON}$=n$\overrightarrow{OC}$(其中0<m,n<1),G为线段MN的中点.