题目内容

如图，平行四边形ABCD中，BD⊥CD，正方形ADEF所在的平面和平面ABCD垂直，H是BE的中点，G是AE，DF的交点．
（1）求证：GH平面CDE；
（2）求证：BD⊥平面CDE．
证明：（1）G是AE，DF的交点，
∴G是AE中点，
又H是BE的中点，
∴△EAB中，GHAB，
∵ABCD，
∴GHCD，
又∵CD平面CDE，GH平面CDE
GH平面CDE
（2）平面ADEF⊥平面ABCD，交线为AD，
∴ED⊥AD，ED平面ADEF
∴ED⊥平面ABCD，
∴ED⊥BD，
又∵BD⊥CD，CD∩ED=D
∴BD⊥平面CDE．
练习册系列答案
相关题目
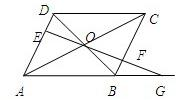精英家教网如图，平行四边形ABCD的对角线交于点O，过点O的直线交AD于E，BC于F，交AB延长线于G，已知AB=a，BC=b，BG=c，则BF=
 
．
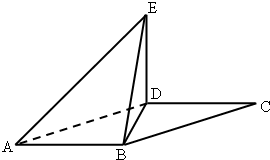精英家教网如图，平行四边形ABCD中，∠DAB=60°，AB=2，AD=4将△CBD沿BD折起到△EBD的位置，使平面EDB⊥平面ABD．
（I）求证：AB⊥DE
（Ⅱ）求三棱锥E-ABD的侧面积．
如图，平行四边形ABCD中，E，F分别是BC，DC的中点，G为交点，若
AB
=
a
，
AD
=
b
，试以
a
，
b
为基底表示
CG
=
-
1
3
(
a
+
b
)
-
1
3
(
a
+
b
)
．
（2012•枣庄一模）如图，平行四边形ABCD中，点E是边BC（靠近点B）的三等分点，F是AB（靠近点A）的三等分点，P是AE与DF的交点，则
AP
用
AB
，
AD
表示为
AP
=
3
10
AB
+
1
10
AD
AP
=
3
10
AB
+
1
10
AD
．
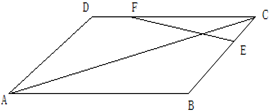精英家教网如图，平行四边形ABCD中，
AB
=
a
，
AD
=
b
，
CE
=
1
3
CB
，
CF
=
2
3
CD
．
（1）用
a
，
b
表示
EF
；
（2）若|
a
|=1，|
b
|=4，∠DAB=60°，分别求|
EF
|和
AC
•
FE
的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网