题目内容
在数列{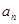 }中,
}中,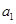 ="13" ,且前
="13" ,且前 项的算术平均数等于第
项的算术平均数等于第 项的2
项的2 -1倍(
-1倍( ∈N*).
∈N*).
(1)写出此数列的前5项;
(2)归纳猜想{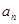 }的通项公式,并用数学归纳法证明.
}的通项公式,并用数学归纳法证明.
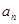 }中,
}中,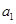 ="13" ,且前
="13" ,且前 项的算术平均数等于第
项的算术平均数等于第 项的2
项的2 -1倍(
-1倍( ∈N*).
∈N*).(1)写出此数列的前5项;
(2)归纳猜想{
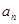 }的通项公式,并用数学归纳法证明.
}的通项公式,并用数学归纳法证明. (1)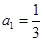 ,
,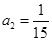 ,
,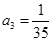 ,
,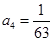 ,
,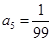
(2)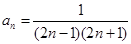 见解析
见解析
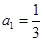 ,
,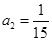 ,
,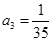 ,
,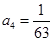 ,
,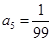
(2)
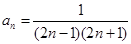 见解析
见解析(1)利用数列{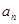 }前
}前 项的算术平均数等于第
项的算术平均数等于第 项的2
项的2 -1倍,推出关系式,通过
-1倍,推出关系式,通过 =2,3,4,5求出此数列的前5项;
=2,3,4,5求出此数列的前5项;
(2)通过(1)归纳出数列{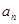 }的通项公式,然后用数学归纳法证明.第一步验证
}的通项公式,然后用数学归纳法证明.第一步验证 =1成立;第二步,假设
=1成立;第二步,假设 =
=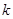 猜想成立,然后证明
猜想成立,然后证明 =
=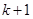 时猜想也成立.
时猜想也成立.
解:(1)由已知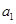 =
= 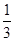 ,
,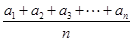 =(2
=(2 -1)
-1)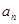 ,分别取
,分别取 =2,3,4,5,得
=2,3,4,5,得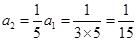 ,
,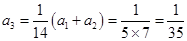 ,
,
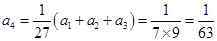 ,
,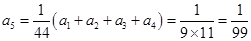 ,
,
所以数列的前5项是: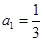 ,
,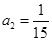 ,
,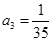 ,
,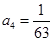 ,
,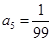 .
.
(2)由(1)中的分析可以猜想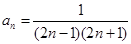 (
( ∈N*).
∈N*).
下面用数学归纳法证明:
①当 =1时,猜想显然成立.
=1时,猜想显然成立.
②假设当 =
=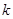 (
(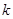 ≥1且
≥1且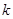 ∈N*)时猜想成立,即
∈N*)时猜想成立,即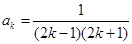 .
.
那么由已知,得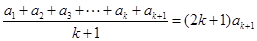 ,
,
即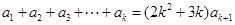 .所以
.所以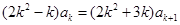 ,
,
即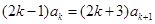 ,又由归纳假设,得
,又由归纳假设,得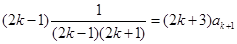 ,
,
所以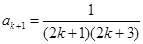 ,即当
,即当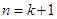 时,猜想也成立.
时,猜想也成立.
综上①和②知,对一切 ∈N*,都有
∈N*,都有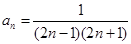 成立.
成立.
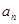 }前
}前 项的算术平均数等于第
项的算术平均数等于第 项的2
项的2 -1倍,推出关系式,通过
-1倍,推出关系式,通过 =2,3,4,5求出此数列的前5项;
=2,3,4,5求出此数列的前5项;(2)通过(1)归纳出数列{
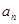 }的通项公式,然后用数学归纳法证明.第一步验证
}的通项公式,然后用数学归纳法证明.第一步验证 =1成立;第二步,假设
=1成立;第二步,假设 =
=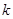 猜想成立,然后证明
猜想成立,然后证明 =
=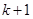 时猜想也成立.
时猜想也成立.解:(1)由已知
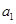 =
= 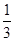 ,
,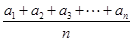 =(2
=(2 -1)
-1)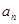 ,分别取
,分别取 =2,3,4,5,得
=2,3,4,5,得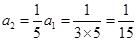 ,
,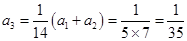 ,
,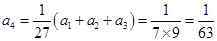 ,
,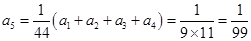 ,
,所以数列的前5项是:
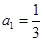 ,
,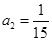 ,
,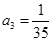 ,
,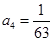 ,
,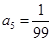 .
.(2)由(1)中的分析可以猜想
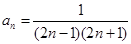 (
( ∈N*).
∈N*). 下面用数学归纳法证明:
①当
 =1时,猜想显然成立.
=1时,猜想显然成立.②假设当
 =
=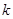 (
(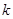 ≥1且
≥1且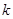 ∈N*)时猜想成立,即
∈N*)时猜想成立,即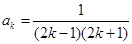 .
.那么由已知,得
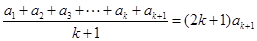 ,
,即
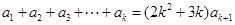 .所以
.所以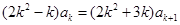 ,
,即
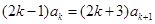 ,又由归纳假设,得
,又由归纳假设,得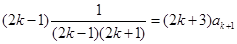 ,
,所以
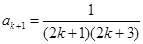 ,即当
,即当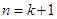 时,猜想也成立.
时,猜想也成立.综上①和②知,对一切
 ∈N*,都有
∈N*,都有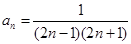 成立.
成立.
练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
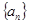 ( n∈N*)中a1>1,公比q>0,设bn=log2an,且b1+b3+b5=6,b1·b3·b5=0.
( n∈N*)中a1>1,公比q>0,设bn=log2an,且b1+b3+b5=6,b1·b3·b5=0.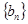 是等差数列;
是等差数列;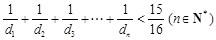 .
.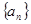 的前
的前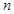 项和记为
项和记为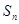 .已知
.已知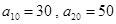 ,
,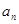 ;(2)若
;(2)若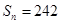 ,求
,求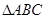 中,角
中,角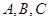 的对边分别为
的对边分别为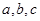 ,且
,且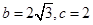 ,求
,求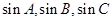 成等比数列,试判断
成等比数列,试判断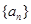 的前n项和
的前n项和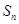 满足
满足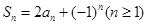
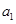 、
、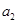 、
、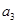 ;
;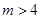 有
有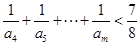
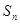 为数列
为数列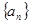 的前n项和,若
的前n项和,若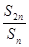
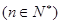 是非零常数,则称该数列为“和等比数列”.若数列
是非零常数,则称该数列为“和等比数列”.若数列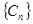 是首项为
是首项为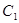 ,公差为
,公差为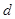 (
(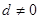 )的等差数列,且数列
)的等差数列,且数列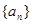 :
: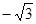 、3、
、3、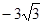 、9、的一个通项公式是( )
、9、的一个通项公式是( ) (
( )
) (
( (
( (
(