题目内容
在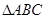 中,角
中,角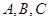 的对边分别为
的对边分别为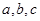 ,且
,且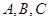 成等差数列
成等差数列
(1)若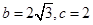 ,求
,求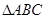 的面积
的面积
(2)若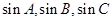 成等比数列,试判断
成等比数列,试判断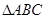 的形状
的形状
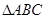 中,角
中,角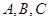 的对边分别为
的对边分别为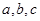 ,且
,且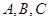 成等差数列
成等差数列(1)若
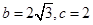 ,求
,求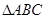 的面积
的面积(2)若
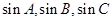 成等比数列,试判断
成等比数列,试判断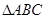 的形状
的形状(1)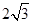 (2)等边三角形.
(2)等边三角形.
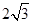 (2)等边三角形.
(2)等边三角形.试题分析:(1)根据A、B、C成等差数列,结合A+B+C=π算出B=
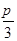 ,再由正弦定理得:
,再由正弦定理得: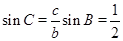 .根据b>c得C为锐角,得到C=
.根据b>c得C为锐角,得到C=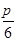 ,从而A=π-B-C=
,从而A=π-B-C=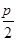 ,△ABC是直角三角形,由此不难求出它的面积.
,△ABC是直角三角形,由此不难求出它的面积.(2)根据正弦定理,结合题意得b2=ac,根据B=
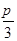 ,利用余弦定理,得b2=a2+c2-ac,从而得到a2+c2-ac=ac,整理得得(a-c)2=0,由此即可得到△ABC为等边三角形.
,利用余弦定理,得b2=a2+c2-ac,从而得到a2+c2-ac=ac,整理得得(a-c)2=0,由此即可得到△ABC为等边三角形.试题解析:∵A、B、C成等差数列,可得2B=A+C.
∴结合A+B+C=π,可得B=
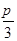 .
.(1)∵
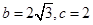 ,
,∴由正弦定理
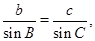 得
得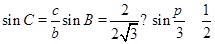 ,
,∵b>c,可得B>C,∴C为锐角,得C=
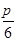 ,从而A=π-B-C=
,从而A=π-B-C=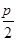 .
.因此,△ABC的面积为S=
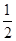 bc=
bc=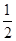 ×
×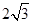 ×2=
×2=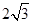 .
.(2)∵sinA、sinB、sinC成等比数列,即sin2B=sinAsinC.
∴由正弦定理,得b2=ac
又∵根据余弦定理,得b2=a2+c2-2accosB=a2+c2-ac,
∴a2+c2-ac=ac,整理得(a-c)2=0,可得a=c
∵B=
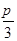 ,∴A=C=
,∴A=C=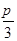 ,可得△ABC为等边三角形.
,可得△ABC为等边三角形.
练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
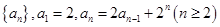
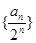 为等差数列;
为等差数列;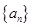 的前n项和
的前n项和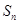 ;
;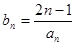 ,求数列
,求数列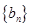 中的最大值.
中的最大值.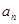 }中,
}中,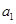 ="13" ,且前
="13" ,且前 项的算术平均数等于第
项的算术平均数等于第 中,
中, ,则通项
,则通项 ___________.
___________. }的前
}的前 项和
项和 ,则
,则 的值为 ;
的值为 ;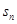 =
=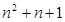 ,那么它的通项公式为an=_________.
,那么它的通项公式为an=_________. 中,
中, ,且
,且 ,则
,则 .
. 满足条件
满足条件 , 则
, 则 = ;
= ;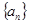 中,首项
中,首项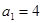 ,公差
,公差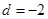 ,则
,则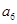 等于( )
等于( )


