题目内容
如图,边长为2的正方形A1ACC1绕直线CC1旋转90°得到正方形B1BCC1,D为CC1的中点,E为A1B的中点,G为△ADB的重心.(1)求直线EG与直线BD所成的角;
(2)求直线A1B与平面ADB所成的角的正弦值.

【答案】分析:(1)以C为坐标原点,CA,CB,CC1所在直线为x,y,z轴,建立空间直角坐标系,分别求出直线EG与直线BD的方向向量,代入向量夹角公式,即可求出答案.
(2)分别求出直线A1B的方向向量与平面ADB的法向量,代入向量夹角公式,即可求出直线A1B与平面ADB所成的角的正弦值.
解答:解:由题设CC1⊥AC,CC1⊥BC,AC⊥BC
所以,以C为坐标原点,CA,CB,CC1所在直线为x,y,z轴,建立空间直角坐标系
则C(0,0,0),A(2,0,0),B(0,2,0),C1(0,0,2),A1(2,0,2),B1(0,2,2),
所以D(0,0,1),E(1,1,1), .(2分)
.(2分)
(1) ,
, (4分)
(4分)
所以 ,
,
∴
所以,直线EG与直线BD所成的角为 .(5分)
.(5分)
(2) (6分)
(6分) ,
,
设 为平面ABD的一个法向量
为平面ABD的一个法向量
则 ,
,
∴
取 .(8分)
.(8分)
设A1B与平面ADB所成的角为θ
则 .
.
即:A1B与平面ADB所成的角为正弦值为 .(10分)
.(10分)
点评:本题考查的知识点是直线与平面所成的角,异面直线及其所成的角,其中建立空间坐标系,把空间异面直线的夹角问题及直线与平面的夹角问题转化为向量夹角问题是解答本题的关键.
(2)分别求出直线A1B的方向向量与平面ADB的法向量,代入向量夹角公式,即可求出直线A1B与平面ADB所成的角的正弦值.
解答:解:由题设CC1⊥AC,CC1⊥BC,AC⊥BC
所以,以C为坐标原点,CA,CB,CC1所在直线为x,y,z轴,建立空间直角坐标系
则C(0,0,0),A(2,0,0),B(0,2,0),C1(0,0,2),A1(2,0,2),B1(0,2,2),
所以D(0,0,1),E(1,1,1),
 .(2分)
.(2分)(1)
 ,
, (4分)
(4分)所以
 ,
,∴

所以,直线EG与直线BD所成的角为
 .(5分)
.(5分)(2)
 (6分)
(6分) ,
,
设
 为平面ABD的一个法向量
为平面ABD的一个法向量则
 ,
,∴

取
 .(8分)
.(8分)设A1B与平面ADB所成的角为θ
则
 .
.即:A1B与平面ADB所成的角为正弦值为
 .(10分)
.(10分)点评:本题考查的知识点是直线与平面所成的角,异面直线及其所成的角,其中建立空间坐标系,把空间异面直线的夹角问题及直线与平面的夹角问题转化为向量夹角问题是解答本题的关键.

练习册系列答案
相关题目
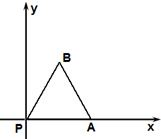 如图放置的边长为1的正三角形PAB沿x轴滚动,设顶点A(x,y)的纵坐标与横坐标的函数关系式是y=f(x),则f(x)在区间[-2,1]上的解析式是
如图放置的边长为1的正三角形PAB沿x轴滚动,设顶点A(x,y)的纵坐标与横坐标的函数关系式是y=f(x),则f(x)在区间[-2,1]上的解析式是 (2011•洛阳一模)如图放置的边长为1的正三角形ABC沿x轴的正方向滚动,设顶点A(x,y)的纵坐标与横坐标的函数关系是y=f(x).则f(x)在两个相邻零点间的图象与x轴围成的面积是
(2011•洛阳一模)如图放置的边长为1的正三角形ABC沿x轴的正方向滚动,设顶点A(x,y)的纵坐标与横坐标的函数关系是y=f(x).则f(x)在两个相邻零点间的图象与x轴围成的面积是 如图所示,过正方形ABCD的中心O作OP⊥平面ABCD,已知正方形的边长为2,OP=2,连接AP、BP、CP、DP,M、N分别是AB、BC的中点,以O为原点,射线OM、ON、OP分别为Ox轴、Oy轴、Oz轴的正方向建立空间直角坐标系.若E、F分别为PA、PB的中点,求A、B、C、D、E、F的坐标.
如图所示,过正方形ABCD的中心O作OP⊥平面ABCD,已知正方形的边长为2,OP=2,连接AP、BP、CP、DP,M、N分别是AB、BC的中点,以O为原点,射线OM、ON、OP分别为Ox轴、Oy轴、Oz轴的正方向建立空间直角坐标系.若E、F分别为PA、PB的中点,求A、B、C、D、E、F的坐标.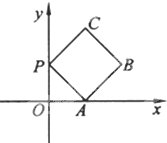 如图放置的边长为2的正方形PABC沿x轴滚动.设顶点P(x,y)的纵坐标与横坐标的函数关系是y=f(x),则f(x)的最小正周期为
如图放置的边长为2的正方形PABC沿x轴滚动.设顶点P(x,y)的纵坐标与横坐标的函数关系是y=f(x),则f(x)的最小正周期为