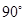题目内容
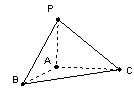
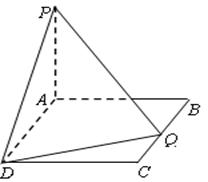
(本小题满分12分)如图,在矩形 中,
中,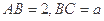 ,又
,又 ⊥平面
⊥平面 ,
,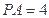 .
.
(Ⅰ)若在边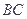 上存在一点
上存在一点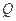 ,使
,使 ,
,
求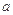 的取值范围;
的取值范围;
(Ⅱ)当边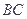 上存在唯一点
上存在唯一点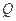 ,使
,使 时,
时,
求二面角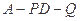 的余弦值.
的余弦值.
 中,
中,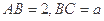 ,又
,又 ⊥平面
⊥平面 ,
,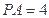 .
.(Ⅰ)若在边
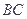 上存在一点
上存在一点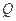 ,使
,使 ,
,求
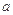 的取值范围;
的取值范围;(Ⅱ)当边
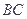 上存在唯一点
上存在唯一点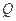 ,使
,使 时,
时,求二面角
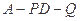 的余弦值.
的余弦值.
解法1:(Ⅰ)如图,连 ,由于PA⊥平面ABCD,则由PQ⊥QD,必有
,由于PA⊥平面ABCD,则由PQ⊥QD,必有 .
.
 ……2分
……2分
设 ,则
,则 ,
,
在 中,有
中,有 .
.
在 中,有
中,有 . ……4分
. ……4分
在 中,有
中,有 .
.
即 ,即
,即 .
.
∴ .
.
故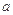 的取值范围为
的取值范围为 . ……6分
. ……6分
(Ⅱ)由(Ⅰ)知,当 ,
, 时,边BC上存在唯一点Q(Q为BC边的中点),使PQ⊥QD.
时,边BC上存在唯一点Q(Q为BC边的中点),使PQ⊥QD.
过Q作QM∥CD交AD于M,则QM⊥AD.
∵PA⊥平面ABCD,∴PA⊥QM.∴QM⊥平面PAD.
过M作MN⊥PD于N,连结NQ,则QN⊥PD.
∴∠MNQ是二面角A-PD-Q的平面角. ……8分
在等腰直角三角形 中,可求得
中,可求得 ,又
,又 ,进而
,进而 .
.
……10分
∴ .
.
故二面角A-PD-Q的余弦值为 . ……12分
. ……12分
 ,由于PA⊥平面ABCD,则由PQ⊥QD,必有
,由于PA⊥平面ABCD,则由PQ⊥QD,必有 .
. ……2分
……2分设
 ,则
,则 ,
,在
 中,有
中,有 .
.在
 中,有
中,有 . ……4分
. ……4分在
 中,有
中,有 .
.即
 ,即
,即 .
.∴
 .
.故
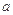 的取值范围为
的取值范围为 . ……6分
. ……6分(Ⅱ)由(Ⅰ)知,当
 ,
, 时,边BC上存在唯一点Q(Q为BC边的中点),使PQ⊥QD.
时,边BC上存在唯一点Q(Q为BC边的中点),使PQ⊥QD. 过Q作QM∥CD交AD于M,则QM⊥AD.
∵PA⊥平面ABCD,∴PA⊥QM.∴QM⊥平面PAD.
过M作MN⊥PD于N,连结NQ,则QN⊥PD.
∴∠MNQ是二面角A-PD-Q的平面角. ……8分
在等腰直角三角形
 中,可求得
中,可求得 ,又
,又 ,进而
,进而 .
.……10分
∴
 .
.故二面角A-PD-Q的余弦值为
 . ……12分
. ……12分略

练习册系列答案
相关题目
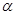 、
、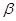 、
、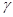 和直线
和直线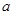 、
、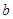 、m、n,下列命题中真命题是( )
、m、n,下列命题中真命题是( ) ,则
,则
 ,则
,则
 ,则
,则
 则
则
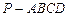 的底面是边长为1的正方形,侧棱
的底面是边长为1的正方形,侧棱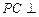 底面
底面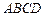 ,且
,且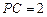 .
. 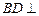 平面
平面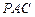
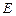 为
为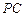 的中点,求二面角
的中点,求二面角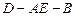 的大小.
的大小.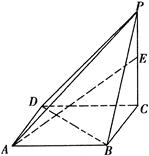




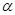 与平面
与平面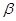 相交,直线
相交,直线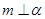 ,则( )
,则( )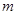 平行,且存在直线与
平行,且存在直线与 )第一题满分5分,第二题满分5分,第三题满分8分.
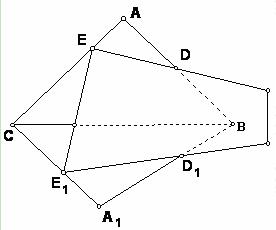
)第一题满分5分,第二题满分5分,第三题满分8分. 条交线ED,CB, E1 D1的关系。
条交线ED,CB, E1 D1的关系。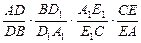 的值;
的值;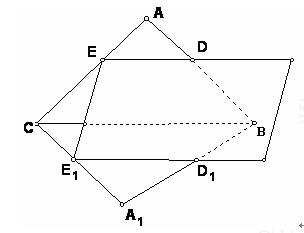
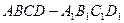 底面
底面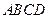 为正方形,
为正方形,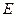 为线段
为线段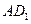 的中点,
的中点,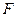 为线段
为线段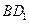 的中点.
的中点. 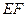 ∥平面
∥平面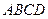 ;
;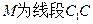 的中点,当
的中点,当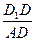 的比值为多少时,
的比值为多少时, 并说明理由.
并说明理由.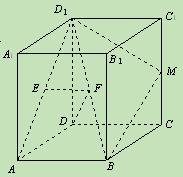
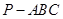 中,
中,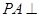 平面
平面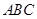 ,
,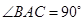 ,
,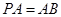 ,则直线
,则直线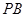 与平面
与平面