题目内容
 如图放置的边长为2的正方形PABC沿x轴滚动.设顶点p(x,y)的轨迹方程是y=f(x),则y=f(x)在其两个相邻零点间的图象与x轴所围成的区域的面积为
如图放置的边长为2的正方形PABC沿x轴滚动.设顶点p(x,y)的轨迹方程是y=f(x),则y=f(x)在其两个相邻零点间的图象与x轴所围成的区域的面积为4π+4
4π+4
.分析:不妨考查沿x轴正方向滚动,先以顶点A为中心顺时针旋转,当顶点B落在x轴上时,再以顶点B为中心顺时针旋转,如此继续,得出函数的图象,即可得到结论.
解答: 解:考查P点的运动轨迹,不妨考查正方形向右滚动,
解:考查P点的运动轨迹,不妨考查正方形向右滚动,
P点从x轴上开始运动的时候,首先是围绕A点运动
个圆,该圆半径为2,
然后以B点为中心,滚动到C点落地,其间是以BP为半径,旋转90°,
再以C为圆心,再旋转90°,这时候以CP为半径,因此最终构成图象如下:
S=2×
×π•22+2×
×2×2+
×π•(2
)2=4π+4.
故答案为:4π+4.
 解:考查P点的运动轨迹,不妨考查正方形向右滚动,
解:考查P点的运动轨迹,不妨考查正方形向右滚动,P点从x轴上开始运动的时候,首先是围绕A点运动
| 1 |
| 4 |
然后以B点为中心,滚动到C点落地,其间是以BP为半径,旋转90°,
再以C为圆心,再旋转90°,这时候以CP为半径,因此最终构成图象如下:
S=2×
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 2 |
故答案为:4π+4.
点评:本题考查的知识点是函数图象的变化,其中根据已知画出正方形转动过程中的一个周期内的图象,利用数形结合的思想对本题进行分析是解答本题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 如图放置的边长为1的正方形ABCD的顶点A、D分别在x轴、y轴(含坐标原点上滑动,则
如图放置的边长为1的正方形ABCD的顶点A、D分别在x轴、y轴(含坐标原点上滑动,则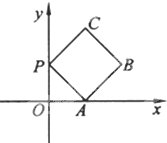 如图放置的边长为2的正方形PABC沿x轴滚动.设顶点P(x,y)的纵坐标与横坐标的函数关系是y=f(x),则f(x)的最小正周期为
如图放置的边长为2的正方形PABC沿x轴滚动.设顶点P(x,y)的纵坐标与横坐标的函数关系是y=f(x),则f(x)的最小正周期为
