题目内容
【题目】已知动圆过定点![]() ,且在
,且在![]() 轴上截得的弦长为
轴上截得的弦长为![]() ,记动圆圆心的轨迹为曲线
,记动圆圆心的轨迹为曲线![]() .
.
(1)求直线![]() 与曲线
与曲线![]() 围成的区域面积;
围成的区域面积;
(2)点![]() 在直线
在直线![]() 上,点
上,点![]() ,过点
,过点![]() 作曲线
作曲线![]() 的切线
的切线![]() 、
、![]() ,切点分别为
,切点分别为![]() 、
、![]() ,证明:存在常数
,证明:存在常数![]() ,使得
,使得![]() ,并求
,并求![]() 的值.
的值.
【答案】(1)![]() ;(2)答案见解析。
;(2)答案见解析。
【解析】试题分析:
(1)根据直接法求得曲线方程为![]() ,解方程组得到直线和曲线C的交点坐标,根据定积分可求得面积.(2)设
,解方程组得到直线和曲线C的交点坐标,根据定积分可求得面积.(2)设![]() 、
、![]() ,结合题意求得切线
,结合题意求得切线![]() 的方程,根据切线方程的特点求出直线
的方程,根据切线方程的特点求出直线![]() 的方程,将直线
的方程,将直线![]() 的方程与
的方程与![]() 联立消元后得到二次方程,根据根与系数的关系求得
联立消元后得到二次方程,根据根与系数的关系求得![]() 和
和![]() 后比较可得
后比较可得![]() ,从而得到结论.
,从而得到结论.
试题解析:
(1) 设动圆圆心的坐标为![]() ,
,
由题意可得![]() ,
,
化简得![]() ,
,
故曲线![]() 的方程为
的方程为![]() .
.
由![]() ,解得
,解得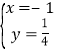 或
或![]() ,
,
所以直线![]() 与曲线
与曲线![]() 围成的区域面积为
围成的区域面积为![]() .
.
(2)设![]() 、
、![]() ,
,
则由题意得切线![]() 的方程为
的方程为![]() ,切线
,切线![]() 的方程为
的方程为![]() ,设点
,设点![]() ,
,
从而有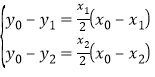 ,
,
所以可得直线AB的方程为![]()
即![]() .
.
由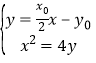 消去y整理得
消去y整理得![]() ,
,
又![]() ,
,
所以![]() ,
,
所以![]() ,
,
故![]() ,
,
![]()
![]()
![]()
= ![]() ,
,
所以![]() .
.
故存在常数![]() ,使得
,使得![]() 成立.
成立.

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案【题目】某幼儿园雏鹰班的生活老师统计2018年上半年每个月的20日的昼夜温差![]() ,
,![]() 和患感冒的小朋友人数(
和患感冒的小朋友人数(![]() /人)的数据如下:
/人)的数据如下:
温差 |
|
|
|
|
|
|
患感冒人数 | 8 | 11 | 14 | 20 | 23 | 26 |
其中![]() ,
,![]() ,
,![]() .
.
(Ⅰ)请用相关系数加以说明是否可用线性回归模型拟合![]() 与
与![]() 的关系;
的关系;
(Ⅱ)建立![]() 关于
关于![]() 的回归方程(精确到
的回归方程(精确到![]() ),预测当昼夜温差升高
),预测当昼夜温差升高![]() 时患感冒的小朋友的人数会有什么变化?(人数精确到整数)
时患感冒的小朋友的人数会有什么变化?(人数精确到整数)
参考数据:![]() .参考公式:相关系数:
.参考公式:相关系数: ,回归直线方程是
,回归直线方程是![]() ,
, ,
,
【题目】每当《我心永恒》这首感人唯美的歌曲回荡在我们耳边时,便会想起电影《泰坦尼克号》中一暮暮感人画面,让我们明白了什么是人类的“真、善、美”.为了推动我市旅游发展和带动全市经济,更为了向外界传递遂宁人民的“真、善、美”.我市某地将按“泰坦尼克号”原型![]() 比例重新修建.为了了解该旅游开发在大众中的熟知度,随机从本市
比例重新修建.为了了解该旅游开发在大众中的熟知度,随机从本市![]() 岁的人群中抽取了
岁的人群中抽取了![]() 人,得到各年龄段人数的频率分布直方图如图所示,现让他们回答问题“该旅游开发将在我市哪个地方建成?”,统计结果如下表所示:
人,得到各年龄段人数的频率分布直方图如图所示,现让他们回答问题“该旅游开发将在我市哪个地方建成?”,统计结果如下表所示:
组号 | 分组 | 回答正确的人数 | 回答正确的人数 占本组的频率 |
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
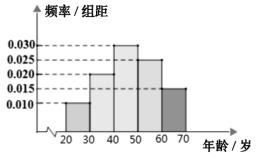
(1)求出![]() 的值;
的值;
(2)从第![]() 组回答正确的人中用分层抽样的方法抽取
组回答正确的人中用分层抽样的方法抽取![]() 人,求第
人,求第![]() 组每组抽取的人数;
组每组抽取的人数;
(3)在(2)中抽取的![]() 人中随机抽取
人中随机抽取![]() 人,求所抽取的人中恰好没有年龄在
人,求所抽取的人中恰好没有年龄在![]() 段的概率.
段的概率.

