Question

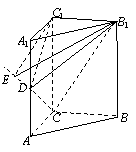
（08年黄冈中学三模）如图，在直三棱柱ABC―A₁B₁C₁中， .

（Ⅰ）若D为AA₁中点，求证：平面B₁CD平面B₁C₁D；

（Ⅱ）若二面角B₁―DC―C₁的大小为60°，求AD的长.

 

 

Answer 1

解析：解法一：（Ⅰ）∵，∴，

又由直三棱柱性质知，∴平面ACC₁A₁.

∴……①

由D为中点可知，，∴

即……②

由①②可知平面B₁C₁D，又平面B₁CD，

故平面平面B₁C₁D.  

（Ⅱ）由（1）可知平面ACC₁A₁，如图，

在面ACC₁A₁内过C₁作，

交CD或延长线或于E，连EB₁，

由三垂线定理可知为二面角B­₁―DC―C₁的平面角，

∴ 

由B₁C₁=2知，，设AD=x，则

∵的面积为1，

     ∴，解得，即

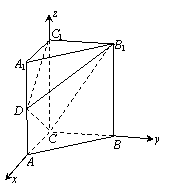
解法二：（Ⅰ）如图，以C为原点，CA、CB、CC₁所在直线为x, y, z轴建立空间直角坐标系.

 则 C（0，0，0），A（1，0，0），B₁（0，2，2），C₁（0，0，2），D（1，0，1）.

即

由，得；

由，得；

又，∴平面B₁C₁D.

又平面B₁CD，

∴平面平面B₁C₁D.  

（Ⅱ）设AD=a，则D点坐标为（1，0，a），，

设平面B₁CD的法向量为. 则由，令z= -1，

得，又平面C₁DC的法向量为，则由，即，故