题目内容
2.(理)将标号为1,2,3,4,5,6的6个小球放入3个不同的盒子中.若每个盒子放2个,其中标号为1,2的小球不能放入同一盒子中,则不同的方法共有72 种.分析 先求出6个小球放入3个盒子,每个盒子中2个的所有种数,再排除其中标号为1,2的球放入同一个盒子的种数,问题得以解决.
解答 解:将6个小球放入3个盒子,每个盒子中2个,有$C_6^2C_4^2C_2^2=90$种情况.其中标号为1,2的球放入同一个盒子中有$C_3^1C_4^2=18$种,
所以满足题意的方法共有90-18=72种.
故答案为:72.
点评 本题考查分步计数原理,考查平均分组问题,是一个易错题,这里包含两个步骤,先平均分组,再排列.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.当实数x,y满足不等式组$\left\{\begin{array}{l}{x+y≥1}\\{y≤1}\\{x-y≤1}\end{array}\right.$,恒有ax+y≤3,则实数a的取值范围是( )
| A. | (-∞,1] | B. | (-∞,-1] | C. | [-1,+∞) | D. | [1,+∞) |
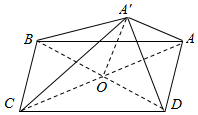 平行四边形ABCD中,AB=$\sqrt{13}$,BC=$\sqrt{5}$,BD=4,AC,BD交于O,将△ABD沿BD折起至△A′BD,使得A′C⊥CB.
平行四边形ABCD中,AB=$\sqrt{13}$,BC=$\sqrt{5}$,BD=4,AC,BD交于O,将△ABD沿BD折起至△A′BD,使得A′C⊥CB.