题目内容
定义方程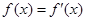 的实数根x0叫做函数
的实数根x0叫做函数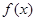 的“新驻点”,如果函数
的“新驻点”,如果函数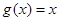 ,
,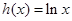 ,
,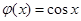 (
(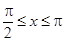 )的“新驻点”分别为
)的“新驻点”分别为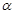 ,
,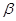 ,
,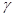 ,那么
,那么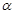 ,
,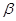 ,
,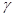 的大小关系是 ( )
的大小关系是 ( )
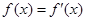 的实数根x0叫做函数
的实数根x0叫做函数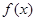 的“新驻点”,如果函数
的“新驻点”,如果函数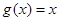 ,
,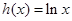 ,
,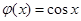 (
(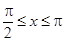 )的“新驻点”分别为
)的“新驻点”分别为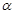 ,
,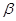 ,
,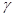 ,那么
,那么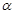 ,
,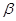 ,
,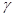 的大小关系是 ( )
的大小关系是 ( ) A.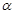 > >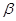 > >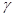 | B.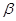 > >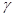 > > | C.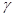 > >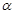 > >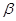 | D.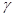 > >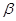 > > |
D
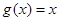 ,则
,则 ,从而有
,从而有 。
。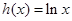 ,则
,则 ,从而有
,从而有 ,记函数
,记函数 ,因为
,因为 ,所以由零点存在定理可知函数
,所以由零点存在定理可知函数 在区间
在区间 内有零点,即
内有零点,即 。
。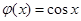 ,则
,则 ,则
,则 。因为
。因为 ,所以
,所以 。所以
。所以 ,故选D
,故选D
练习册系列答案
 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
 ,
, ,1.5634="5.968" ).
,1.5634="5.968" ). 的图象如下图所示,则函数
的图象如下图所示,则函数 的单调减区间是( )
的单调减区间是( )




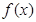 是R上的奇函数,且当
是R上的奇函数,且当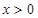 时,
时,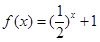 ,则
,则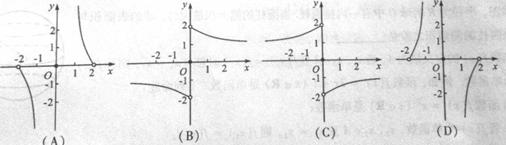
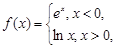 则
则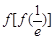 = ( )
= ( )
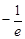

 至少有一个方程有实数根,求实数
至少有一个方程有实数根,求实数 的取值范围.
的取值范围.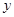 (万元)与机器运转时间
(万元)与机器运转时间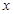 (年数,
(年数,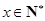 )的关系为
)的关系为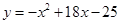 .则当每台机器运转 年时,年平均利润最大,最大值是 万元.
.则当每台机器运转 年时,年平均利润最大,最大值是 万元.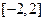 上的
上的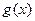 为奇函数,且在区间
为奇函数,且在区间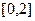 上单调递增,则满足
上单调递增,则满足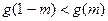 的
的 的取值范围为____ ▲ __
的取值范围为____ ▲ __