题目内容
已知,f(x)=xlnx,g(x)=ax2+bx-1,函数y=g(x)的导数g′(x)的图象如图所示.
(Ⅰ)求g(x)的解析式;
(Ⅱ)d≥f(x)-g(x)对一切x>0恒成立,求实数d的取值范围;
(Ⅲ)设h(x)=f(x)-g(x),求函数h(x)的零点个数.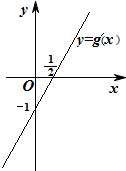
(Ⅰ)求g(x)的解析式;
(Ⅱ)d≥f(x)-g(x)对一切x>0恒成立,求实数d的取值范围;
(Ⅲ)设h(x)=f(x)-g(x),求函数h(x)的零点个数.
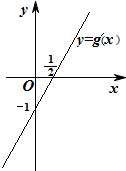
解(Ⅰ)∵g(x)=ax2+bx-1,∴g'(x)=2ax+b
由图可知b=-1,∴g'(x)=2ax-1,
将x=
,y=0代入计算得a=1,
∴g(x)=x2-x-1.…3分
(Ⅱ)设T(x)=lnx-x+1(x>0).
∴T′(x)=
-1=
,∴当0<x<1时,T'(x)>0,T(x)单调递增,当x>1时,T'(x)<0,T(x)单调递减.
∴T(x)max=T(x)极大=T(1)=0,即对一切x>0,都有lnx-x+1≤0,
∴xlnx-x2+x≤0,即xlnx-x2+x+1≤1.
由(Ⅰ)得f(x)-g(x)=xlnx-x2+x+1,所以对一切x>0都有f(x)-g(x)≤1.
所以实数求d的取值范围是[1,+∞).…8分
(Ⅲ)h(x)=xlnx-x2+x+1,h'(x)=lnx-2x+2(x>0).
设t(x)=lnx-2x+2(x>0),则t′(x)=-
,所以当0<x<
时,t'(x)>0,h'(x)=t(x)是增函数,当x>
时,t'(x)<0,h'(x)=t(x)是减函数,所以h′(x)max=h′(
)=1-ln2>0.
又h'(e-2)=-2e-2<0,所以在区间(e-2,
)上存在唯一的实数x0,使得h'(x0)=t'(1)=0(e是自然对数的底数),
所以当x变化时,h'(x)、h(x)的变化情况如下表:
∴h(x)极小=h(x0)=x0lnx0-
+x0+1,且h'(x0)=lnx0-2x0+2=0,∴h(x)极小=h(x0)=x0(2x0-2)-
+x0+1=
-x0+1=(x0-
)2+
>0.
∵h(x)在区间(1,+∞)递减,h(e)=2e-e2+1<0,∴在区间(1,e)上存在唯一一点x,使得h(x)=0.
综上所述,函数h(x)的零点个数是1.…14分.
由图可知b=-1,∴g'(x)=2ax-1,
将x=
| 1 |
| 2 |
∴g(x)=x2-x-1.…3分
(Ⅱ)设T(x)=lnx-x+1(x>0).
∴T′(x)=
| 1 |
| x |
| 1-x |
| x |
∴T(x)max=T(x)极大=T(1)=0,即对一切x>0,都有lnx-x+1≤0,
∴xlnx-x2+x≤0,即xlnx-x2+x+1≤1.
由(Ⅰ)得f(x)-g(x)=xlnx-x2+x+1,所以对一切x>0都有f(x)-g(x)≤1.
所以实数求d的取值范围是[1,+∞).…8分
(Ⅲ)h(x)=xlnx-x2+x+1,h'(x)=lnx-2x+2(x>0).
设t(x)=lnx-2x+2(x>0),则t′(x)=-
2(x-
| ||
| 2x2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又h'(e-2)=-2e-2<0,所以在区间(e-2,
| 1 |
| 2 |
所以当x变化时,h'(x)、h(x)的变化情况如下表:
| x | (0,x0) | x0 | (x0,1) | 1 | (1,+∞) |
| h'(x) | - | 0 | + | 0 | - |
| h(x) | ↘ | 极小值 | ↗ | 极大值1 | ↘ |
| x | 20 |
| x | 20 |
| x | 20 |
| 1 |
| 2 |
| 3 |
| 4 |
∵h(x)在区间(1,+∞)递减,h(e)=2e-e2+1<0,∴在区间(1,e)上存在唯一一点x,使得h(x)=0.
综上所述,函数h(x)的零点个数是1.…14分.

练习册系列答案
相关题目
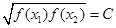 ,则称函数f(x)在D上的几何平均数为C.已知f(x)=x3,x∈[1,2],则函数f(x)=x3在[1,2]上的几何平均数为
,则称函数f(x)在D上的几何平均数为C.已知f(x)=x3,x∈[1,2],则函数f(x)=x3在[1,2]上的几何平均数为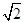 B.2 C.4
D. 2
B.2 C.4
D. 2 ,方程f(x)=x有唯一的解,
,方程f(x)=x有唯一的解, .
. )是等差数列;
)是等差数列; ,求Sn=b1+b2+b3+…+bn
,求Sn=b1+b2+b3+…+bn 成立,若存在,求出m的值;若不存在,请说明理由。
成立,若存在,求出m的值;若不存在,请说明理由。