题目内容
设椭圆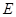 :
: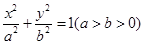 的左、右焦点分别为
的左、右焦点分别为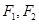 ,已知椭圆
,已知椭圆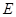 上的任意一点
上的任意一点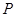 ,满足
,满足 ,过
,过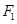 作垂直于椭圆长轴的弦长为3.
作垂直于椭圆长轴的弦长为3.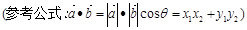
(1)求椭圆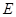 的方程;
的方程;
(2)若过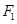 的直线交椭圆于
的直线交椭圆于 两点,求
两点,求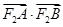 的取值范围.
的取值范围.
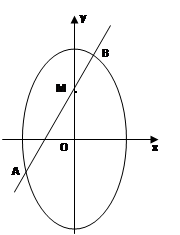
(1)  (2)
(2) 
解析试题分析:解:(1)设点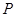
 ,则
,则 ,
, ,
,
 ,又
,又 ,
, ,∴椭圆的方程为:
,∴椭圆的方程为:
(2)当过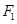 直线
直线 的斜率不存在时,点
的斜率不存在时,点 ,则
,则 ;
;
当过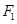 直线
直线 的斜率存在时,设斜率为
的斜率存在时,设斜率为 ,则直线
,则直线 的方程为
的方程为 ,设
,设
由 得:
得:


综合以上情形,得:
考点:椭圆的方程、几何性质
点评: 本小题主要考查椭圆的方程、几何性质,平面向量的数量积的坐标运算,直线与圆锥曲线的位置关系等基本知识及推理能力和运算能力

练习册系列答案
相关题目
 轴上,且过点
轴上,且过点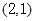 .
.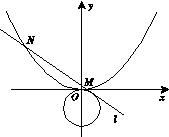
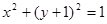 相切的直线
相切的直线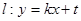 交抛物线于不同的两点
交抛物线于不同的两点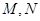 若抛物线上一点
若抛物线上一点 满足
满足
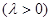 ,求
,求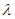 的取值范围.
的取值范围.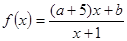 在
在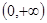 上是增函数;命题q:方程
上是增函数;命题q:方程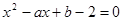 有两个不相等的负实数根。求使得p
有两个不相等的负实数根。求使得p q是真命题的实数对
q是真命题的实数对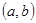 为坐标的点的轨迹图形及其面积。
为坐标的点的轨迹图形及其面积。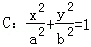 的右焦点F,抛物线:
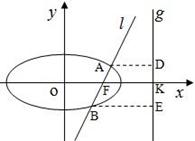
的右焦点F,抛物线: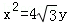 的焦点为椭圆C的上顶点,且直线l交椭圆C于A、B两点,点A、F、B在直线g:x=4上的射影依次为点D、K、E.(1)椭圆C的方程;(2)直线l交y轴于点M,且
的焦点为椭圆C的上顶点,且直线l交椭圆C于A、B两点,点A、F、B在直线g:x=4上的射影依次为点D、K、E.(1)椭圆C的方程;(2)直线l交y轴于点M,且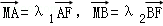 ,当m变化时,探求λ1+λ2的值是否为定值?若是,求出λ1+λ2的值,否则,说明理由;(3)接AE、BD,试证明当m变化时,直线AE与BD相交于定点
,当m变化时,探求λ1+λ2的值是否为定值?若是,求出λ1+λ2的值,否则,说明理由;(3)接AE、BD,试证明当m变化时,直线AE与BD相交于定点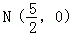 .
.
 .
.
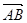 所成的比为2,求线段AB所在直线的方程.
所成的比为2,求线段AB所在直线的方程. =λ
=λ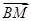 .
.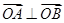 ;
;  两个顶点
两个顶点 的坐标分别是
的坐标分别是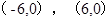 ,边
,边 所在直线的斜率之积等于
所在直线的斜率之积等于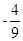 ,求顶点
,求顶点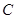 的轨迹方程,并画出草图。
的轨迹方程,并画出草图。 的方程为
的方程为 它的离心率为
它的离心率为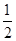 ,一个焦点是(-1,0),过直线
,一个焦点是(-1,0),过直线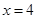 上一点引椭圆
上一点引椭圆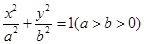 上的点
上的点 处的切线方程是
处的切线方程是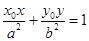 .求证:直线AB恒过定点C,并求出定点C的坐标;
.求证:直线AB恒过定点C,并求出定点C的坐标;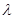 ,使得求证:
,使得求证: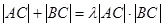 (点C为直线AB恒过的定点).若存在
(点C为直线AB恒过的定点).若存在 (
(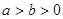 ),点
),点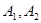 为椭圆C的左、右顶点。
为椭圆C的左、右顶点。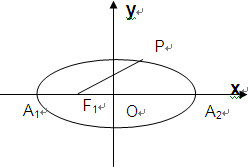
 与(1)中所述椭圆C相交于A、B两点(A、B不是左、右顶点),且满足
与(1)中所述椭圆C相交于A、B两点(A、B不是左、右顶点),且满足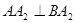 ,求证:直线
,求证:直线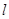 过定点,并求出该点的坐标。
过定点,并求出该点的坐标。