题目内容
设命题p:函数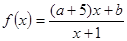 在
在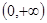 上是增函数;命题q:方程
上是增函数;命题q:方程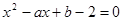 有两个不相等的负实数根。求使得p
有两个不相等的负实数根。求使得p q是真命题的实数对
q是真命题的实数对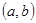 为坐标的点的轨迹图形及其面积。
为坐标的点的轨迹图形及其面积。
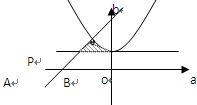
实数对(a,b)为坐标的点的轨迹图形如图(阴影部分, 不包括边界。),S=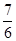 。
。
解析试题分析: f(x) =
f(x) =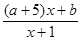 ,p真
,p真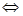 f ′(x)=
f ′(x)= 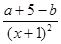 >0
>0
对于x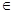 (0,+
(0,+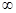 )成立
)成立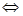 a-b+5>0。
a-b+5>0。
q真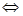 方程x2-ax+b-2=0有两个不相等的负实数根
方程x2-ax+b-2=0有两个不相等的负实数根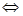
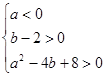 …………4分
…………4分
p q是真命题
q是真命题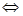 p真且q真
p真且q真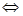


实数对(a,b)为坐标的点的轨迹图形如图(阴影部分, 不包括边界。) 8分
解: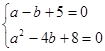 得a1= -2,a2= 6, 解
得a1= -2,a2= 6, 解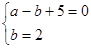 得a=" -3;"
得a=" -3;" 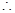 (a,b)为坐标的点的轨迹图形的面积:
(a,b)为坐标的点的轨迹图形的面积:
S=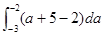 +
+ =
=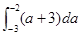 +
+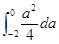 11分
11分
=( a2+3a)|
a2+3a)| +
+ 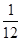 a3|
a3|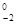 =
=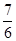 13分
13分
考点:本题主要考查利用导数研究函数的单调性,二次函数的零点的分布,复合命题真值表,定积分计算,简单线性规划。
点评:中档题,涉及命题的题目,往往综合性较强,需要综合应用数学知识的解题。本题综合考查了利用导数研究函数的单调性,二次函数的零点的分布,复合命题真值表,定积分计算,简单线性规划等。

练习册系列答案
相关题目
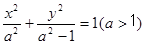 的左右焦点为
的左右焦点为 ,抛物线C:
,抛物线C: 以F2为焦点且与椭圆相交于点
以F2为焦点且与椭圆相交于点 、
、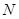
 ,点
,点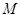 在
在 轴上方,直线
轴上方,直线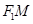 与抛物线
与抛物线 相切.
相切.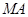 ,
, 与
与 轴分别交于点
轴分别交于点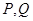 .
.  是以
是以 ,
,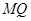 为腰的等腰三角形,探究直线AB的斜率是否为定值?若是求出这个定值,若不是说明理由.
为腰的等腰三角形,探究直线AB的斜率是否为定值?若是求出这个定值,若不是说明理由.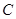 :
: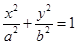
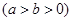 的离心率为
的离心率为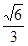 ,过右焦点
,过右焦点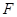 且斜率为
且斜率为 的直线交椭圆
的直线交椭圆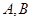 两点,
两点,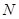 为弦
为弦 的中点,
的中点, 为坐标原点.
为坐标原点.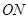 的斜率
的斜率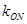 ;
;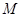 ,都存在
,都存在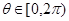 ,使得
,使得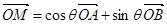 成立.
成立.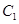 的中心在坐标原点,两个焦点分别为
的中心在坐标原点,两个焦点分别为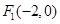 ,
,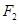
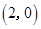 ,点
,点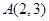 在椭圆
在椭圆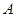 的直线
的直线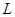 与抛物线
与抛物线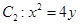 交于
交于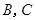 两点,抛物线
两点,抛物线 在点
在点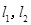 ,且
,且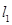 与
与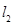 交于点
交于点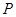 .
. 的点
的点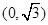 ,曲线C的参数方程为
,曲线C的参数方程为 (φ为参数)。以原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
(φ为参数)。以原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为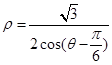 。
。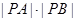 的值。
的值。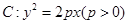 的焦点为
的焦点为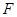 ,经过点
,经过点 交抛物线
交抛物线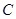 于点
于点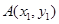 ,
,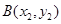 且
且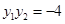 .
.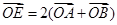 (
( 为坐标原点),且点
为坐标原点),且点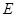 在抛物线
在抛物线 是抛物线
是抛物线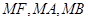 的斜率分别为
的斜率分别为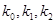 .求证:
.求证: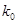 为定值时,
为定值时,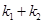 也为定值.
也为定值.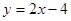 与抛物线
与抛物线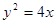 交于
交于 两点.
两点. 的长;(2)若抛物线
的长;(2)若抛物线 ,求
,求 的值.
的值. :
: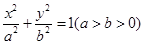 的左、右焦点分别为
的左、右焦点分别为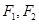 ,已知椭圆
,已知椭圆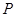 ,满足
,满足 ,过
,过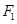 作垂直于椭圆长轴的弦长为3.
作垂直于椭圆长轴的弦长为3.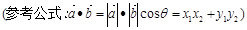
 两点,求
两点,求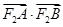 的取值范围.
的取值范围.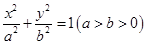 的离心率
的离心率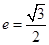 ,且短半轴
,且短半轴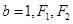 为其左右焦点,
为其左右焦点,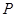 是椭圆上动点.
是椭圆上动点.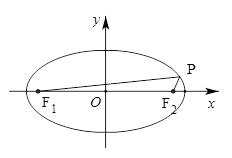
 时,求
时,求 面积;
面积;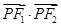 取值范围.
取值范围.