Question

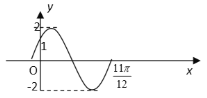
【题目】光线从点射出，到轴上的点后，被轴反射到轴上的点，又被轴反射，这时反射线恰好过点.

（1）求所在直线的方程；

（2）过点且斜率为的直线与，轴分别交于、，过、作直线的垂线，垂足为、，求线段长度的最小值.

Answer 1

【答案】（1）；（2）.

【解析】

（1）根据光线的反射原理，点关于轴对称点以及点关于轴对称点均在在直线上，即可求解；

（2）先求出直线的点斜式方程，进而得到坐标，根据已知可得，为两平行线的距离，求出直线方程，得到两平行线的距离，利用基本不等式即可求解.

（1）点关于轴对称为，

点关于轴对称点为，

直线经过，两点，

故直线，

即为所求的直线方程.

（2）设的方程为，

令，令

即，.

从而可得直线和的方程分别为

和，

又，为两平行线的距离，

，∴.

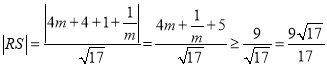当且仅当等号成立.