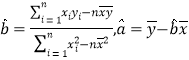题目内容
【题目】某体育公司对最近6个月内的市场占有率进行了统计,结果如表:

(1)可用线性回归模型拟合![]() 与
与![]() 之间的关系吗?如果能,请求出
之间的关系吗?如果能,请求出![]() 关于
关于![]() 的线性回归方程,如果不能,请说明理由;
的线性回归方程,如果不能,请说明理由;
(2)公司决定再采购![]() ,
,![]() 两款车扩大市场,
两款车扩大市场,![]() ,
,![]() 两款车各100辆的资料如表:
两款车各100辆的资料如表:

平均每辆车每年可为公司带来收入500元,不考虑采购成本之外的其他成本,假设每辆车的使用寿命都是整数年,用每辆车使用寿命的频率作为概率,以每辆车产生利润的期望值作为决策依据,应选择采购哪款车型?
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() .
.
参考公式:相关系数 ;
;
回归直线方程![]() ,其中
,其中 ,
,![]() .
.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】分析:(1)先计算相关系数 越接近于1则代表线性关系越强即可判断;(2)用频率估计概率,分别求出
越接近于1则代表线性关系越强即可判断;(2)用频率估计概率,分别求出![]() 、B款车的利润的分布列求出期望即可作出选择.
、B款车的利润的分布列求出期望即可作出选择.
(1)∵![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴
![]() ,
,
所以两变量之间具有较强的线性相关关系,
故可用线性回归模型拟合两变量之间的关系.
 ,
,
又![]() ,
,![]() ,
,
∴![]() ,
,
∴回归直线方程为![]() .
.
(2)用频率估计概率,![]() 款车的利润
款车的利润![]() 的分布列为:
的分布列为:
|
|
|
|
|
|
|
|
|
|
∴![]() (元).
(元).
![]() 款车的利润
款车的利润![]() 的分布列为:
的分布列为:
|
|
|
|
|
|
|
|
|
|
∴![]() (元).
(元).
以每辆车产生利润俄期望值为决策依据,故应选择![]() 款车型.
款车型.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
【题目】从某工厂的一个车间抽取某种产品![]() 件,产品尺寸(单位:
件,产品尺寸(单位:![]() )落在各个小组的频数分布如下表:
)落在各个小组的频数分布如下表:
数据分组 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
|
(1)根据频数分布表,求该产品尺寸落在![]() 的概率;
的概率;
(2)求这![]() 件产品尺寸的样本平均数
件产品尺寸的样本平均数![]() ;(同一组中的数据用该组区间的中点值作代表)
;(同一组中的数据用该组区间的中点值作代表)
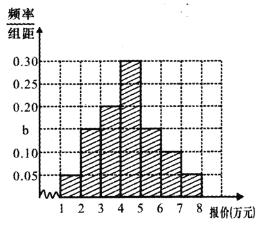
(3)根据频数分布对应的直方图,可以认为这种产品尺寸![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为样本平均值
近似为样本平均值![]() ,
,![]() 近似为样本方差
近似为样本方差![]() ,经过计算得
,经过计算得![]() ,利用该正态分布,求
,利用该正态分布,求![]() .
.
附:①若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ;②
;②![]() .
.