题目内容
定义在(-1,l)上的函数f (x)满足:当x,y∈(-1,l)时,f(x)-f (y)=f(
),并且当x∈(-1,0)时,f (x)>0;若P=f(
)+f(
),Q=f(
),R=f(0),则P,Q,R的大小关系为( )
| x-y |
| 1-xy |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2 |
| A.R>Q>P | B.R>P>Q | C.P>Q>R | D.Q>P>R |
∵x,y∈(-1,l)时,f(x)-f (y)=f(
),
令y=x=0可得f(0)-f(0)=f(0)
∴f(0)=0
令x=0可得f(0)-f(y)=f(-y),即f(-y)=-f(y)
∴f(-x)=-f(x)
∴函数f(x)是奇函数
设-1<x1<x2<0
则-1<x1-x2<0,0<1-x1x2<1
∴-1<(
)<0
∴f(x1)-f(x2)=f(
)>0
即f(x1)>f(x2)
∴f(x)在(-1,0)上是单调减函数
根据奇函数的对称区间上的单调性相反可知,函数f(x)在(-1,1)上单调 递减
而P=f(
)+f(
)=f(
)-f(-
)=f(
)=f(
)
由于
>
>0,
由单调性可得R>Q>P
故选A
| x-y |
| 1-xy |
令y=x=0可得f(0)-f(0)=f(0)
∴f(0)=0
令x=0可得f(0)-f(y)=f(-y),即f(-y)=-f(y)
∴f(-x)=-f(x)
∴函数f(x)是奇函数
设-1<x1<x2<0
则-1<x1-x2<0,0<1-x1x2<1
∴-1<(
| x1-x2 |
| 1-x1x2 |
∴f(x1)-f(x2)=f(
| x1-x2 |
| 1-x1x2 |
即f(x1)>f(x2)
∴f(x)在(-1,0)上是单调减函数
根据奇函数的对称区间上的单调性相反可知,函数f(x)在(-1,1)上单调 递减
而P=f(
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 4 |
| ||||
1+
|
| 7 |
| 13 |
由于
| 7 |
| 13 |
| 1 |
| 2 |
由单调性可得R>Q>P
故选A

练习册系列答案
相关题目
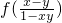 ,并且当x∈(-1,0)时,f (x)>0;若P=f(
,并且当x∈(-1,0)时,f (x)>0;若P=f( )+f(
)+f( ),Q=f(
),Q=f( ),R=f(0),则P,Q,R的大小关系为
),R=f(0),则P,Q,R的大小关系为 ,并且当x∈(-1,0)时,f (x)>0;若P=f(
,并且当x∈(-1,0)时,f (x)>0;若P=f( )+f(
)+f( ),Q=f(
),Q=f( ),R=f(0),则P,Q,R的大小关系为( )
),R=f(0),则P,Q,R的大小关系为( )