题目内容

对定义在［-1，1］上的函数f(x)，若存在常数M＞0，使得对任意x1、x2∈［-1,1］，都有|f(x1)-f(x2)|≤M|x1-x2|,则称f(x)具有性质L，试问函数f(x)=x2+2x+3是否具有性质L？证明你的结论.

解析：函数f(x)=x2+2x+3具有性质L.

证明：由|f(x1)-f(x2)|=|x12-x22+2(x1-x2)|=|x1-x2||x1+x2+2|≤|x1-x2|(|x1|+|x2|+2)≤4|x1-x2|,

∴存在M=4，使f(x)具有性质L.

练习册系列答案
相关题目
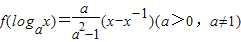定义在（-1，1）上的函数f（x），对任意的x，y∈（-1，1）都有：f(x)+f(y)=f(
x+y
1+xy
)；且当x∈（-∞，0）时，f（x）＞0，回答下列问题：
（1）判断函数f（x）在（-1，1）的奇偶性，并说明理由；
（2）判断函数f（x）在（-1，1）的单调性，并说明理由；
（3）若f(
1
5
)=
1
2
，试求f(
1
2
)-f(
1
11
)-f(
1
19
)的值．
已知函数f（x）满足f(logax)=
aa2-1
(x-x-1)(a＞0，a≠1)，
（Ⅰ）求f（x）的解析式并判断其单调性；
（Ⅱ）对定义在（-1，1）上的函数f（x），若f（1-m）+f（1-m2）＜0，求m的取值范围；
（Ⅲ）当x∈（-∞，2）时，关于x的不等式f（x）-4＜0恒成立，求a的取值范围．
定义在（-1，1）上的函数f（x）满足：①对任意x，y∈(-1，1)有f(x)-f(y)=f(
x-y
1-xy
)，②当x∈（-1，0）时，有f（x）＞0；若P=f(
1
5
)+f(
1
11
)+…+f(
1
r2+r-1
)+…+f(
1
20092+2009-1
)，Q=f(
1
2
)，R=f（0），则P，Q，R的大小关系为
Q＜P＜R
Q＜P＜R
（用“＜”连接）
定义在区间[-1，1]上的奇函数f（x）满足：对任意a，b∈[-1，1]，a+b≠0，都有
f(a)+f(b)a+b
＜0，f（1）=-3．
（1）证明：f（x）在[-1，1]上是减函数；
（2）解不等式：f（x+1）+f（x2-1）＞0；
（3）若不等式f（x）≤m2+2am对任意x，a∈[-1，1]恒成立，求实数m的取值范围．
已知函数f（x）满足，
（Ⅰ）求f（x）的解析式并判断其单调性；
（Ⅱ）对定义在（-1，1）上的函数f（x），若f（1-m）+f（1-m2）＜0，求m的取值范围；
（Ⅲ）当x∈（-∞，2）时，关于x的不等式f（x）-4＜0恒成立，求a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网