Question

【题目】设函数定义域为，对于区间，如果存在，，使得，则称区间为函数的区间.

（Ⅰ）判断是否是函数的区间;

（Ⅱ）若是函数（其中）的区间，求的取值范围;

（Ⅲ）设为正实数，若是函数的区间，求的取值范围.

Answer 1

【答案】（Ⅰ）见证明；（Ⅱ） （Ⅲ）

【解析】

Ⅰ根据新定义，即可求出判断，

Ⅱ根据新定义和对数函数的性质，即可求出a的取值范围，

Ⅲ根据新定义和余弦函数的性质可得存在k，，使得，再分类讨论即可求出的取值范围

（Ⅰ）不是函数的区间，理由如下：

因为 对，，

所以 .

所以 均有，

即不存在，，使得.

所以不是函数的区间

（Ⅱ）由是函数（其中的区间，可知

存在，，使得.

所以 .

因为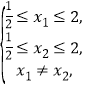

所以 ，即.

又因为 且，

所以 .

（Ⅲ）因为 是函数的区间，

所以 存在，，使得.

所以

所以 存在，使得

不妨设. 又因为 ，

所以 .

所以 .

即在区间内存在两个不同的偶数.

①当时，区间的长度，

所以 区间内必存在两个相邻的偶数，故符合题意.

②当时，有，

所以 .

（i）当时，有即.

所以 也符合题意.

（ii）当时，有即.

所以 符合题意.

（iii）当时，有即此式无解.

综上所述，的取值范围是.