题目内容
关于x的不等式ax2+bx+21＜0的解集为{x|-7＜x＜-1}，求关于x的不等式x2+（a-1）x-b＞0的解集．
考点：一元二次不等式的解法
专题：不等式的解法及应用
分析：由关于x的不等式ax2+bx+21＜0的解集，结合根与系数的关系，求出a、b的值，再求不等式x2+（a-1）x-b＞0的解集．
解答：
解：∵关于x的不等式ax2+bx+21＜0的解集为{x|-7＜x＜-1}，
∴
；
解得a=3，b=24；
不等式x2+（a-1）x-b＞0化为
x2+2x-24＞0；
解得x＜-6或x＞4，
∴该不等式的解集为（-∞，-6）∪（4，∞）．
∴
|
解得a=3，b=24；
不等式x2+（a-1）x-b＞0化为
x2+2x-24＞0；
解得x＜-6或x＞4，
∴该不等式的解集为（-∞，-6）∪（4，∞）．
点评：本题考查了一元二次不等式的解法与应用问题，也考查了根与系数的关系的应用问题，是基础题．
练习册系列答案
相关题目
已知a=0.70.8，b=log20.8，c=1.10.8，则a，b，c的大小关系是（ ）
| A、a＜b＜c |
| B、b＜a＜c |
| C、a＜c＜b |
| D、b＜c＜a |
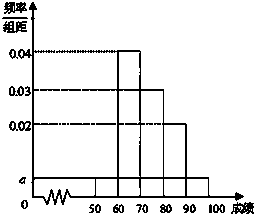某校100名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100]．