题目内容
已知函数
，(1)求函数的单调区间；(2)当
时，求函数的最大值与最小值。
解：(1) 
由
，得
，
函数单调递增；同理，
或
函数单调递减. （４分）
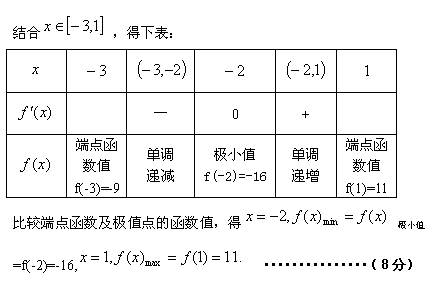(2)由①
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
每日10分钟口算心算速算天天练系列答案题目内容
已知函数，(1)求函数的单调区间；(2)当时，求函数的最大值与最小值。
解：(1) 由，得，函数单调递增；同理，或函数单调递减. （４分）
(2)由①
每日10分钟口算心算速算天天练系列答案
．
，不计算函数值，求
．
与
的大小．
时，求函数
的单调区间;
，试问函数
在
上是否存在保值区间？若存在，请求出一个保值区间；若不存在，请说明理由.
的定义域；
为何值时，函数值大于1.
，
，
，
这几个函数值，你能发现f（x）与
有什么关系？并证明你的结论；
的值；
在区间（0，+∞）上的单调性．
，求
的大小