题目内容
已知θ是三角形的一个内角，且sinθ、cosθ是关于x的方程2x2+px-1=0的两根，则θ等于
- A.
- B.
- C.
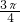
- D.
C
分析：利用韦达定理，结合同角三角函数平方关系，即可得出结论．
解答：∵sinθ、cosθ是关于x的方程2x2+px-1=0的两根，
∴
∴①2-②×2，可得
∴p=0
∴sinθ+cosθ=0
∵θ是三角形的一个内角，
∴θ=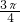
故选C．
点评：本题考查三角函数的求值，考查韦达定理的运用，考查学生的计算能力，属于基础题．
分析：利用韦达定理，结合同角三角函数平方关系，即可得出结论．
解答：∵sinθ、cosθ是关于x的方程2x2+px-1=0的两根，
∴
∴①2-②×2，可得
∴p=0
∴sinθ+cosθ=0
∵θ是三角形的一个内角，
∴θ=
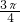
故选C．
点评：本题考查三角函数的求值，考查韦达定理的运用，考查学生的计算能力，属于基础题．
练习册系列答案
相关题目
是三角形的一个内角，且
，则
的值为（ ）
B．
C．
D．