题目内容
已知向量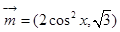 ,
,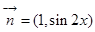 ,函数
,函数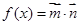 .
.
(1)求函数 的最小正周期和单调增区间;
的最小正周期和单调增区间;
(2)在
 中,
中,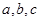 分别是角
分别是角 的对边,R为
的对边,R为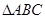 外接圆的半径,且
外接圆的半径,且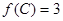 ,
,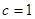 ,
,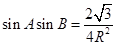 ,且
,且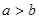 ,求
,求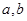 的值.
的值.
(1)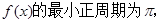
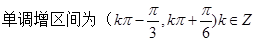
(2)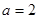 ,
,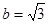
解析试题分析:(1)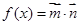
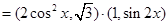
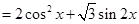

 , ……3分
, ……3分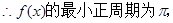 ……4分
……4分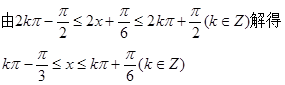
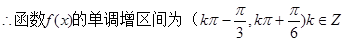 . ……6分
. ……6分
(2)
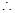

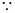
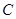 是三角形内角, ∴
是三角形内角, ∴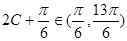 , ∴
, ∴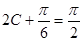
即: ……9分
……9分
∴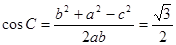 即:
即: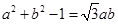 , ……10分
, ……10分
由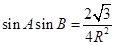 可得:
可得: 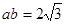 得:
得: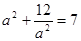 解之得:
解之得: ,
,
∴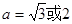 所以当
所以当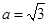 时,
时,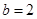 ; 当
; 当 ,
,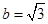 ,
, 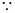
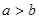
∴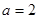 ,
,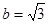 . ……12分
. ……12分
考点:本小题主要考查向量的数量积计算,三角函数的化简和求值,三角函数图象和性质的应用,以及正弦定理余弦定理的应用,考查学生的运算求解能力和综合运算公式解决问题的能力.
点评:三角函数与平面向量问题是每年高考的必考题目,一般涉及到平面向量的运算,三角函数的化简求值和三角函数图象和性质的应用,要牢固掌握三角函数中众多公式,灵活运用公式解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
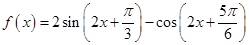 .
.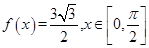 时的
时的 的集合;
的集合;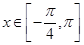 时,求函数
时,求函数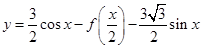 的最值.
的最值.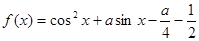 .
. ≤
≤ ≤
≤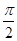 时,用
时,用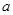 表示
表示 的最大值
的最大值 ;
;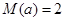 时,求
时,求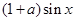 在
在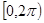 上有两解?
上有两解?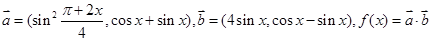
 的解析式;
的解析式; 轴的正半轴及
轴的正半轴及 轴的正半轴三者围成图形的面积。
轴的正半轴三者围成图形的面积。 (其中
(其中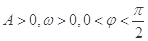 )的图像如图所示.
)的图像如图所示.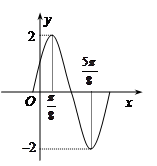
 的解析式;
的解析式;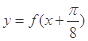 的零点.
的零点.
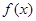 的最小正周期;
的最小正周期; ,求函数
,求函数 ,其中
,其中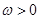 .
. ,求函数f(x)的最小正周期;
,求函数f(x)的最小正周期; 满足
满足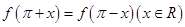 ,且
,且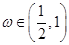 ,求函数f(x)的单调递减区间.
,求函数f(x)的单调递减区间. ,
, ],f(x)=tan2x+2tan x+2,求f(x)的最大值和最小值,并求出相应的x值.
],f(x)=tan2x+2tan x+2,求f(x)的最大值和最小值,并求出相应的x值. 已知函数
已知函数 ,
, .
.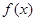 的最小正周期和单调递增区间;
的最小正周期和单调递增区间; 上的最小值和最大值,并求出取得最值时
上的最小值和最大值,并求出取得最值时 的值.
的值.