题目内容
设集合A={a,a2,b+1},B={0,|a|,b}且A=B.
(1)求a,b的值;
(2)判断函数f(x)=-bx-
在[1,+∞)的单调性,并用定义加以证明.
(1)求a,b的值;
(2)判断函数f(x)=-bx-
| a |
| x |
(1)两集合相等,观察发现a不能为O,故只有b+1=0,得b=-1,故b与a对应,所以a=-1,
故a=-1,b=-1
(2)由(1)得f(x)= x+
,在[1,+∞)是增函数
任取x1,x2∈[1,+∞)令x1<x2,
f(x1)-f(x2)=x1+
-x2-
=(x1-x2)(1-
)
∵1≤x1<x2,
∴x1-x2<0,又x1x2>1,故1-
>0
∴f(x1)-f(x2)=(x1-x2)(1-
)<0
∴f(x1)<f(x2)
故f(x)= x+
,在[1,+∞)是增函数
故a=-1,b=-1
(2)由(1)得f(x)= x+
| 1 |
| x |
任取x1,x2∈[1,+∞)令x1<x2,
f(x1)-f(x2)=x1+
| 1 |
| x1 |
| 1 |
| x2 |
| 1 |
| x1x2 |
∵1≤x1<x2,
∴x1-x2<0,又x1x2>1,故1-
| 1 |
| x1x2 |
∴f(x1)-f(x2)=(x1-x2)(1-
| 1 |
| x1x2 |
∴f(x1)<f(x2)
故f(x)= x+
| 1 |
| x |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
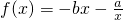 在[1,+∞)的单调性,并用定义加以证明.
在[1,+∞)的单调性,并用定义加以证明.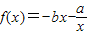 在[1,+∞)的单调性,并用定义加以证明.
在[1,+∞)的单调性,并用定义加以证明.