题目内容
设集合A={a,a2,b2-1},B={0,|a|,b},且A=B,求a,b的值.
分析:由两个集合相等的条件找出a和b的关系列出方程求出a,b,再代入集合中进行检验即可得.
解答:解:由于0∈B,且A={a,a2,b2-1},
∴a=0或a2=0或b2-1=0
解得a=0或b=-1或b=1,
当a=0时,B集合不满足集合的互异性,(舍去)
当b=-1时,A={a,a2,0},B={0,|a|,-1},∴a=-1,此时,A={-1,1,0},B={0,1,-1},满足A=B,所以a=-1,b=-1,
当b=1时,A={a,a2,0},B={0,|a|,1},∴a=-1或a=1,不满足集合的互异性,舍去,
此时,A={-1,1,0},B={0,1,-1},满足A=B,所以a=-1,b=-1,
综上所述,a=-1,b=-1.
∴a=0或a2=0或b2-1=0
解得a=0或b=-1或b=1,
当a=0时,B集合不满足集合的互异性,(舍去)
当b=-1时,A={a,a2,0},B={0,|a|,-1},∴a=-1,此时,A={-1,1,0},B={0,1,-1},满足A=B,所以a=-1,b=-1,
当b=1时,A={a,a2,0},B={0,|a|,1},∴a=-1或a=1,不满足集合的互异性,舍去,
此时,A={-1,1,0},B={0,1,-1},满足A=B,所以a=-1,b=-1,
综上所述,a=-1,b=-1.
点评:本题考查的是集合元素与集合的关系问题.在解答时应充分体会集合中元素的特点、元素与集合关系的应用以及多解检验等知识,特别是问题转化的解题思想在此题解答中起到重要的作用,非常值得同学们反思和归纳.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
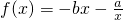 在[1,+∞)的单调性,并用定义加以证明.
在[1,+∞)的单调性,并用定义加以证明.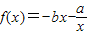 在[1,+∞)的单调性,并用定义加以证明.
在[1,+∞)的单调性,并用定义加以证明.