题目内容
设集合A={a,a2,b+1},B={0,|a|,b}且A=B.
(1)求a,b的值;
(2)判断函数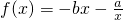 在[1,+∞)的单调性,并用定义加以证明.
在[1,+∞)的单调性,并用定义加以证明.
解:(1)两集合相等,观察发现a不能为O,故只有b+1=0,得b=-1,故b与a对应,所以a=-1,
故a=-1,b=-1
(2)由(1)得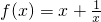 ,在[1,+∞)是增函数
,在[1,+∞)是增函数
任取x1,x2∈[1,+∞)令x1<x2,
f(x1)-f(x2)=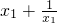 -
-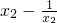 =(x1-x2)(1-
=(x1-x2)(1- )
)
∵1≤x1<x2,
∴x1-x2<0,又x1x2>1,故1- >0
>0
∴f(x1)-f(x2)=(x1-x2)(1- )<0
)<0
∴f(x1)<f(x2)
故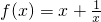 ,在[1,+∞)是增函数
,在[1,+∞)是增函数
分析:(1)求,b的值,由于两集合相等,观察发现其对应特征,建立方程求出a,b的值
(2)将a,b的值代入,先判断单调性,再用定义法证明即可.
点评:本题考查集合相等的概念以及函数单调性的证明方法--定义法,解答第二小问时要注意步骤,先判断再证明,注意格式.
故a=-1,b=-1
(2)由(1)得
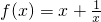 ,在[1,+∞)是增函数
,在[1,+∞)是增函数任取x1,x2∈[1,+∞)令x1<x2,
f(x1)-f(x2)=
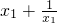 -
-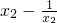 =(x1-x2)(1-
=(x1-x2)(1- )
)∵1≤x1<x2,
∴x1-x2<0,又x1x2>1,故1-
 >0
>0∴f(x1)-f(x2)=(x1-x2)(1-
 )<0
)<0∴f(x1)<f(x2)
故
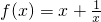 ,在[1,+∞)是增函数
,在[1,+∞)是增函数分析:(1)求,b的值,由于两集合相等,观察发现其对应特征,建立方程求出a,b的值
(2)将a,b的值代入,先判断单调性,再用定义法证明即可.
点评:本题考查集合相等的概念以及函数单调性的证明方法--定义法,解答第二小问时要注意步骤,先判断再证明,注意格式.

练习册系列答案
相关题目
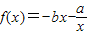 在[1,+∞)的单调性,并用定义加以证明.
在[1,+∞)的单调性,并用定义加以证明.