题目内容
已知曲线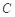 的极坐标方程是
的极坐标方程是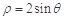 ,直线的参数方程是
,直线的参数方程是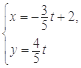 (为参数).
(为参数).
设直线与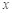 轴的交点是
轴的交点是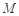 ,
,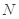 是曲线
是曲线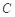 上一动点,求
上一动点,求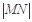 的最大值.
的最大值.
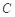 的极坐标方程是
的极坐标方程是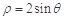 ,直线的参数方程是
,直线的参数方程是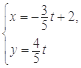 (为参数).
(为参数).设直线与
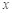 轴的交点是
轴的交点是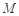 ,
,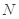 是曲线
是曲线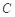 上一动点,求
上一动点,求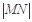 的最大值.
的最大值.
试题分析:首先将曲线
 的极坐标方程、直线的参数方程转化为直角坐标方程,可知,曲线
的极坐标方程、直线的参数方程转化为直角坐标方程,可知,曲线 是以
是以 为圆心,1为半径的圆,由直线的直角坐标方程得,令
为圆心,1为半径的圆,由直线的直角坐标方程得,令 ,可求出点
,可求出点 的坐标,则点
的坐标,则点 与圆心
与圆心 的距离
的距离 可以求,从而可得曲线
可以求,从而可得曲线 上的动点
上的动点 与定点
与定点 的最大值为
的最大值为 .
.试题解析:曲线
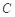 的直角坐标方程为
的直角坐标方程为 ,故圆
,故圆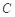 的圆心坐标为(0,1),半径
的圆心坐标为(0,1),半径
直线l的直角坐标方程
 , 令
, 令 ,得
,得 ,即
,即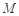 点的坐标为(2,0).
点的坐标为(2,0). 从而
 ,所以
,所以 .即
.即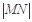 的最大值为
的最大值为 。
。
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的参数方程为
的参数方程为 (
( 为参数),曲线
为参数),曲线 的极坐标方程
的极坐标方程 .
. 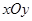 中,曲线
中,曲线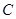 的参数方程为
的参数方程为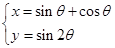 (
(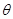 为参数),若以直角坐标系
为参数),若以直角坐标系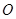 点为极点,
点为极点,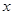 轴正方向为极轴,且长度单位相同,建立极坐标系,得直线
轴正方向为极轴,且长度单位相同,建立极坐标系,得直线 的极坐标方程为
的极坐标方程为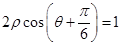 .求直线
.求直线 =1上找一点,使这一点到直线x-2y-12=0的距离最小.
=1上找一点,使这一点到直线x-2y-12=0的距离最小. (θ为参数,0≤θ<2π)上求一点,使它到直线C2:
(θ为参数,0≤θ<2π)上求一点,使它到直线C2: (t为参数)的距离最小,并求出该点坐标和最小距离.
(t为参数)的距离最小,并求出该点坐标和最小距离. (t为参数)过椭圆C:
(t为参数)过椭圆C: (φ为参数)的右顶点,则常数a的值为 .
(φ为参数)的右顶点,则常数a的值为 . (t为参数),若点P(m,2)在曲线C上,求m的值.
(t为参数),若点P(m,2)在曲线C上,求m的值.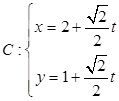 (
(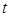 为参数)的普通方程为___________.
为参数)的普通方程为___________.