题目内容
已知函数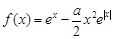 .
.
(Ⅰ)若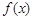 是
是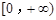 上是增函数,求实数a的取值范围;
上是增函数,求实数a的取值范围;
(Ⅱ)证明:当a≥1时,证明不等式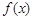 ≤x+1对x∈R恒成立;
≤x+1对x∈R恒成立;
(Ⅲ)对于在(0,1)中的任一个常数a,试探究是否存在x0>0,使得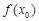 >x0+1成立?如果存在,请求出符合条件的一个x0;如果不存在,请说明理由.
>x0+1成立?如果存在,请求出符合条件的一个x0;如果不存在,请说明理由.
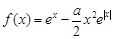 .
.(Ⅰ)若
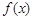 是
是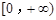 上是增函数,求实数a的取值范围;
上是增函数,求实数a的取值范围;(Ⅱ)证明:当a≥1时,证明不等式
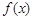 ≤x+1对x∈R恒成立;
≤x+1对x∈R恒成立;(Ⅲ)对于在(0,1)中的任一个常数a,试探究是否存在x0>0,使得
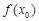 >x0+1成立?如果存在,请求出符合条件的一个x0;如果不存在,请说明理由.
>x0+1成立?如果存在,请求出符合条件的一个x0;如果不存在,请说明理由.(I)a的取值范围为a≤0;(Ⅱ)详见解析;(Ⅲ)可找到一个常数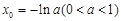 ,使得
,使得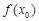 >x0+1成立.
>x0+1成立.
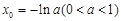 ,使得
,使得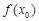 >x0+1成立.
>x0+1成立. 试题分析:(I)
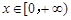 时,
时,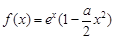 ,求导得
,求导得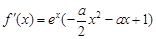 .由题意,
.由题意,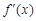 ≥0在
≥0在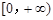 上恒成立.因为ex>0恒成立,故只需
上恒成立.因为ex>0恒成立,故只需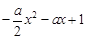 ≥0在
≥0在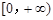 上恒成立,结合抛物线的图象即可得a的取值范围;(Ⅱ)由题知f(x)≤x+1即为
上恒成立,结合抛物线的图象即可得a的取值范围;(Ⅱ)由题知f(x)≤x+1即为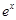 -
-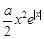 ≤x+1.由于含有
≤x+1.由于含有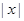 ,故分
,故分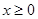 和
和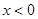 两种情况讨论.①在x≥0时,要证明
两种情况讨论.①在x≥0时,要证明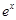 -
-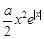 ≤x+1成立,可变为证1≤
≤x+1成立,可变为证1≤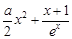 成立,这样只需利用导数求
成立,这样只需利用导数求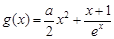 的最小值即可,求导得
的最小值即可,求导得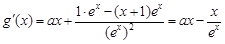 ,易得
,易得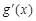 ≥0,从而g(x)≥g(0)=1.注:直接证
≥0,从而g(x)≥g(0)=1.注:直接证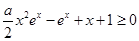 也可,只是需要求两次导数.
也可,只是需要求两次导数.②在x≤0时,要证
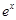 -
-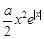 ≤x+1成立,可变为证1≤
≤x+1成立,可变为证1≤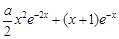 成立,这样只需利用导数求
成立,这样只需利用导数求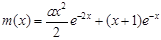 的最小值即可.
的最小值即可.(Ⅲ)要使f(x0)>x0+1成立,即
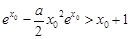 .如果变为
.如果变为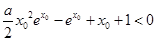 ,那么求导后式子很复杂,故尝试作其它的变形.
,那么求导后式子很复杂,故尝试作其它的变形.变形为
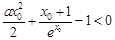 ,要找一个x0>0使该不等式成立,只需找到函数
,要找一个x0>0使该不等式成立,只需找到函数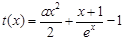 的最小值,满足
的最小值,满足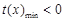 即可.这利用导数就容易解决了.
即可.这利用导数就容易解决了.试题解析:(I)∵
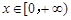 时,
时,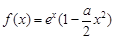 ,
,∴
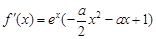 .
.由题意,
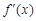 ≥0在
≥0在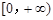 上恒成立,
上恒成立,当a=0时,
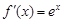 >0恒成立,即满足条件.
>0恒成立,即满足条件.当a≠0时,要使
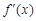 ≥0,而ex>0恒成立,
≥0,而ex>0恒成立,故只需
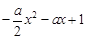 ≥0在
≥0在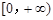 上恒成立,即
上恒成立,即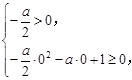 解得a<0.
解得a<0.综上,a的取值范围为a≤0. 4分
(Ⅱ)由题知f(x)≤x+1即为
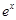 -
-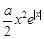 ≤x+1.
≤x+1.①在x≥0时,要证明
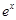 -
-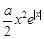 ≤x+1成立,
≤x+1成立,只需证
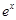 ≤
≤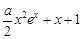 ,即证1≤
,即证1≤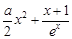 , ①
, ①令
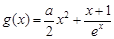 ,得
,得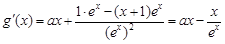 ,
,整理得
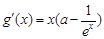 ,
,∵x≥0时,
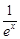 ≤1,结合a≥1,得
≤1,结合a≥1,得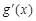 ≥0,
≥0,∴
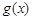 为在
为在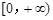 上是增函数,故g(x)≥g(0)=1,从而①式得证.
上是增函数,故g(x)≥g(0)=1,从而①式得证.②在x≤0时,要使
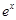 -
-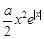 ≤x+1成立,
≤x+1成立,只需证
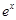 ≤
≤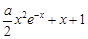 ,即证1≤
,即证1≤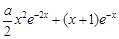 , ②
, ②令
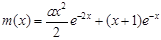 ,得
,得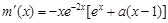 ,
,而
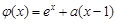 在x≤0时为增函数,
在x≤0时为增函数,故
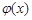 ≤
≤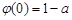 ≤0,从而
≤0,从而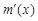 ≤0,
≤0,∴m(x)在x≤0时为减函数,则m(x)≥m(0)=1,从而②式得证.
综上所述,原不等式
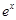 -
-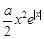 ≤x+1即f(x)≤x+1在a≥1时恒成立. 10分
≤x+1即f(x)≤x+1在a≥1时恒成立. 10分(Ⅲ)要使f(x0)>x0+1成立,即
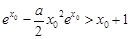 ,
,变形为
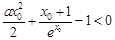 , ③
, ③要找一个x0>0使③式成立,只需找到函数
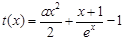 的最小值,满足
的最小值,满足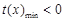 即可.
即可.∵
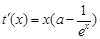 ,
,令
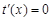 得
得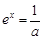 ,则x=-lna,取x0=-lna,
,则x=-lna,取x0=-lna,在0<x<-lna时,
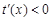 ,在x>-lna时,
,在x>-lna时,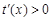 ,
,即t(x)在(0,-lna)上是减函数,在(-lna,+∞)上是增函数,
∴当x=-lna时,
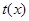 取得最小值
取得最小值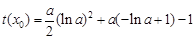
下面只需证明:
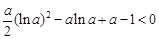 在
在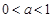 时成立即可.
时成立即可.又令
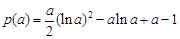 ,
,则
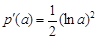 ≥0,从而
≥0,从而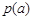 在(0,1)上是增函数,
在(0,1)上是增函数,则
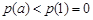 ,从而
,从而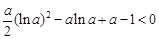 ,得证.
,得证.于是
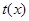 的最小值
的最小值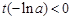 ,
,因此可找到一个常数
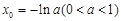 ,使得③式成立. 14分
,使得③式成立. 14分
练习册系列答案
相关题目
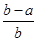 <ln
<ln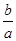 <
<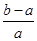 ,其中0<a<b;
,其中0<a<b;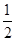 + +
+ +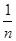 ]≤1+[lnn](n∈N*).
]≤1+[lnn](n∈N*).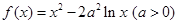 .
.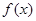 的单调区间;
的单调区间;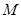 ,求证:
,求证: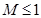 .
.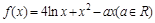 .
.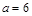 时,求函数
时,求函数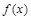 的单调区间;
的单调区间;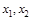 ,且
,且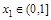 ,求证:
,求证: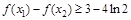 ;
;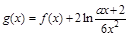 ,对于任意
,对于任意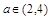 时,总存在
时,总存在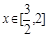 ,使
,使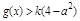 成立,求实数
成立,求实数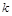 的取值范围.
的取值范围.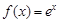 ,
,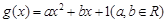 .
.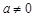 ,则
,则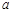 ,
,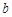 满足什么条件时,曲线
满足什么条件时,曲线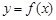 与
与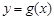 在
在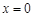 处总有相同的切线?
处总有相同的切线?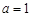 时,求函数
时,求函数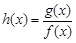 的单调减区间;
的单调减区间;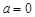 时,若
时,若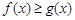 对任意的
对任意的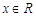 恒成立,求
恒成立,求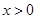 ,函数
,函数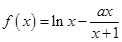 .
.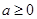 时,讨论函数
时,讨论函数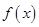 的单调性;
的单调性;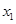 和
和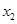 )时,求证:
)时,求证: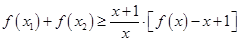 .
.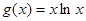 .
.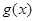 在
在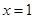 处的切线方程;
处的切线方程;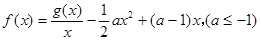 的单调区间;
的单调区间;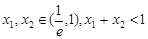 ,求证:
,求证: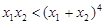 .
.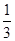 x3-2x2+3m,x∈[0,+∞),若f(x)+5≥0恒成立,则实数m的取值范围是________.
x3-2x2+3m,x∈[0,+∞),若f(x)+5≥0恒成立,则实数m的取值范围是________.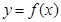 为R上的可导函数,当
为R上的可导函数,当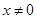 时,
时,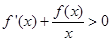 ,则函数
,则函数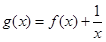 的零点分数为( )
的零点分数为( )