题目内容

在空间四边形OABC中，
OA
=
a
，
OB
=
b
，
OC
=
c
，点M在线段OA上，且OM=2MA，N为BC的中点，则
MN
等于（　　）
分析：由题意结合图形，直接利用
MN
=
ON
+
MO
，求出
ON
，然后即可解答．
解答：解：因为空间四边形OABC如图，
OA
=
a
，
OB
=
b
，
OC
=
c
，
点M在线段OA上，且OM=2MA，N为BC的中点，
所以
ON
=
1
2
c
+
1
2
b
．
所以
MN
=
ON
+
MO
=-
2
3
a
+
1
2
b
  +
1
2
c
．
故选B．
点评：本题考查空间向量的基本运算，考查计算能力．
练习册系列答案
相关题目
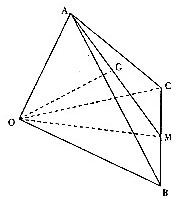精英家教网如图，在空间四边形OABC中，M，G分别是BC，AM的中点，设
OA
=
a
，
OB
=
b
，
OC
=
c
．
（1）用基底{
a
 ， 
b
 ，
c
}表示向量
OG
；
（2）若|
a
|=|
b
|=|
c
|=
3
，且
a
与
b
、
c
夹角的余弦值均为
1
3
，
b
与
c
夹角为60°，求|
OG
|．
（理科试题）如图，在空间四边形OABC中，G是△ABC的重心，若
OG
=x
OA
+y
OB
+z
OC
，则x+y+z=
1
1
．
在空间四边形OABC中，OA=8，AB=6，AC=4，BC=5，∠OAC=45°，∠OAB=60°．则异面直线AO与BC的夹角的余弦值为
1
5
(3-2
2
)
1
5
(3-2
2
)
．
如图，在空间四边形OABC中，已知E是线段BC的中点，G为AE的中点，若
OA
，
OB
，
OC
分别记为
a
，
b
，
c
，则用
a
，
b
，
c
表示
OG
的结果为
OG
=
1
2
a
+
1
4
b
+
1
4
c
1
2
a
+
1
4
b
+
1
4
c
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网