题目内容
如图,正三棱柱 中,点
中,点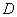 是
是 的中点.
的中点.

(Ⅰ)求证:  平面
平面 ;
;
(Ⅱ)求证:  平面
平面 .
.
(Ⅰ)详见解析;(Ⅱ)详见解析.
【解析】
试题分析:(Ⅰ)欲证线面垂直,先考察线线垂直,易知 和
和 ,所以
,所以 平面
平面 ;(Ⅱ)线面平行,先构造线线平行,根据中点,易想到构造三角形中位线,连接
;(Ⅱ)线面平行,先构造线线平行,根据中点,易想到构造三角形中位线,连接 ,设
,设 ,则可达到目的
,则可达到目的 .
.


试题解析:(Ⅰ)因为 是正三角形,而点
是正三角形,而点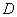 是
是 的中点,所以
的中点,所以 3分
3分
又三棱柱 是正三棱柱,所以
是正三棱柱,所以 面
面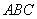 ,
, 面
面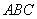 ,所以
,所以 ,
, ,所以
,所以 平面
平面 ; 7分
; 7分
(Ⅱ)连接 ,设
,设 ,则
,则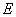 为
为 的中点,连接
的中点,连接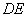 ,由
,由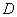 是
是 的中点,
的中点,
得 11分
11分
又 面
面 ,且
,且 面
面 ,所以
,所以 平面
平面 . 14分
. 14分
考点:直线与平面平行的判定、直线与平面垂直的判定.

练习册系列答案
相关题目
已知 的三内角
的三内角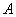 、
、 、
、 所对的边分别是
所对的边分别是 ,
, ,
, ,向量
,向量 =(cosB,cosC),
=(cosB,cosC), =(2a+c,b),且
=(2a+c,b),且 ⊥
⊥ .
.
(1)求角 的大小;
的大小;
(2)若 ,求
,求 的范围
的范围
|
| A | B | C |
| A | 7 | 20 | 5 |
| B | 9 | 18 | 6 |
| C |
| 4 |
|
 有公共点,则b的取值范围是 .
有公共点,则b的取值范围是 . 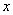
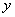
 与平面
与平面 夹角的余弦值是( )
夹角的余弦值是( ) B.
B.  C.
C. D.
D.
 y2=1上一动点,O为坐标原点,M为线段OP的中点,则点M的轨迹方程是 .
y2=1上一动点,O为坐标原点,M为线段OP的中点,则点M的轨迹方程是 . 是
是 有实根的( )
有实根的( ) 的公差不为零,首项
的公差不为零,首项 ,
, 是
是 和
和 的等比中项,则数列的前项
的等比中项,则数列的前项 之和是 ( )
之和是 ( ) B.
B. C.
C. D.
D.
 轴上,一个顶点为
轴上,一个顶点为 ,且其右焦点到直线
,且其右焦点到直线 的距离为3.
的距离为3. ,与椭圆交于两个不同的点
,与椭圆交于两个不同的点 ,且满足
,且满足 ,求直线的方程.
,求直线的方程. 中,三个内角
中,三个内角 所对的边分别为
所对的边分别为

 ,
, .
. ;
; 求
求 的值.
的值.