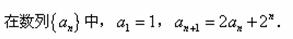题目内容
已知椭圆的中心在原点,焦点在 轴上,一个顶点为
轴上,一个顶点为 ,且其右焦点到直线
,且其右焦点到直线 的距离为3.
的距离为3.
(1)求椭圆方程;
(2)设直线过定点 ,与椭圆交于两个不同的点
,与椭圆交于两个不同的点 ,且满足
,且满足 ,求直线的方程.
,求直线的方程.
 那么
那么 ,∴椭圆方程为
,∴椭圆方程为 .
.
(2)若直线斜率不存在时,直线即为 轴,此时
轴,此时 为椭圆的上下顶点,
为椭圆的上下顶点,
 ,不满足条件;
,不满足条件;
故可设直线: ,与椭圆
,与椭圆 联立,
联立,
消去 得:
得:  .
.
由 ,得
,得 .
.
由韦达定理得
而
设 的中点
的中点 ,则
,则
由 ,则有
,则有 .
.



练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,则( )
,则( ) 中,点
中,点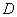 是
是 的中点.
的中点.
 平面
平面 ;
; 平面
平面 .
. 的离心率为
的离心率为 ,则C的渐近线方程为( )
,则C的渐近线方程为( ) x (B)y=±
x (B)y=± x (C)y=±
x (C)y=± x (D)y=±x
x (D)y=±x
 的左焦点,
的左焦点,
 是双曲线右支上的动点,则
是双曲线右支上的动点,则
 的最小值为 .
的最小值为 . 由
由 确定,则方程
确定,则方程 的实数解有( )
的实数解有( ) 的零点,若
的零点,若 ,则
,则 的值满足
的值满足 B.
B. C.
C. D.
D. 及以下3个函数:①
及以下3个函数:① ;
; ;③
;③ 其中图像能等分圆
其中图像能等分圆 面积的函数有
面积的函数有 个 B.
个 B.  个 C.
个 C.  个 D.
个 D.  个
个