题目内容

△ABC中,A、B、C所对三边为a、b、c,B(-1,0)、C(1,0),求满足sinC-sinB=sinA的顶点A的轨迹.

解析:∵sinC-sinB=sinA,∴=·,

即c-b=×2=1,即|AB|-|AC|=1.

∴动点A(x,y)符合双曲线的定义,且知双曲线中的2a=1,2c=2.

∴a=,b2=c2-a2=.

∴点A的轨迹方程是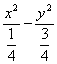=1(x＞).

由c＞b即|AB|＞|AC|,可知点A的轨迹是以B、C为焦点,实轴长为1,虚轴长为3的双曲线的右支,还需去掉点(,0).

练习册系列答案
相关题目
△ABC中A，B为锐角sinA-sinB=
1-
3
2
，cosA-cosB=
3
-1
2
．
（1）试通过计算判断△ABC的形状．
（2）求角A，B的值．
在△ABC中A＞B，则下列不等式中不一定正确的是（　　）
正弦定理（默写）
a
sinA
=
b
sinB
=
c
sinC
=2R（a，b，c为△ABC中∠A，∠B，∠C的对边，R为△ABC外接圆半径）
a
sinA
=
b
sinB
=
c
sinC
=2R（a，b，c为△ABC中∠A，∠B，∠C的对边，R为△ABC外接圆半径）
．
（2009•红桥区二模）在△ABC中a，b，c分别是角A，B，C的对边，bcosC，acosA，ccosB成等差数列，a=
3
，b+c=3，求：
（Ⅰ）角A；
（Ⅱ）△ABC的面积．
（2012•淮北二模）在△ABC中a，b，c分别为角A，B，C所对的边的边长．
（1）试叙述正弦或余弦定理并证明之；
（2）设a+b+c=1，求证：a2+b2+c2≥
13
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网