题目内容
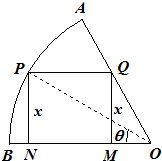 如图,在半径为
如图,在半径为| 3 |
(1)按下列要求写出函数的关系式:
①设PN=x,将y表示成x的函数关系式;
②设∠POB=θ,将y表示成θ的函数关系式;
(2)请你选用(1)中的一个函数关系式,求出y的最大值.
分析:( 1)①通过求出矩形的边长,求出面积的表达式;
②利用三角函数的关系,求出矩形的邻边,求出面积的表达式;
(2)利用(1)②的表达式,化为一个角的一个三角函数的形式,根据θ的范围确定矩形面积的最大值.
②利用三角函数的关系,求出矩形的邻边,求出面积的表达式;
(2)利用(1)②的表达式,化为一个角的一个三角函数的形式,根据θ的范围确定矩形面积的最大值.
解答:解:(1)①因为ON=
,OM=
x,所以MN=
-
x,(2分)
所以y=x(
-
x) x∈(0,
).(4分)
②因为PN=
sinθ,ON=
cosθ,OM=
×
sinθ =sinθ,
所以MN=ON-OM=
cosθ-sinθ(6分)
所以y=
sinθ(
cosθ-sinθ),
即y=3sinθcosθ-
sin2θ,θ∈(0,
)(8分)
(2)选择y=3sinθcosθ-
sin2θ=
sin(2θ+
)-
,(12分)
∵θ∈(0,
)∴2θ+
∈(
,
)(13分)
所以ymax=
.(14分)
| 3-x2 |
| ||
| 3 |
| 3-x2 |
| ||
| 3 |
所以y=x(
| 3-x2 |
| ||
| 3 |
| 3 |
| 2 |
②因为PN=
| 3 |
| 3 |
| ||
| 3 |
| 3 |
所以MN=ON-OM=
| 3 |
所以y=
| 3 |
| 3 |
即y=3sinθcosθ-
| 3 |
| π |
| 3 |
(2)选择y=3sinθcosθ-
| 3 |
| 3 |
| π |
| 6 |
| ||
| 2 |
∵θ∈(0,
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
所以ymax=
| ||
| 2 |
点评:本题是中档题,考查函数解析式的求法,三角函数的最值的确定,三角函数公式的灵活运应,考查计算能力,课本题目的延伸.如果选择①需要应用导数求解,麻烦,不是命题者的本意.

练习册系列答案
相关题目
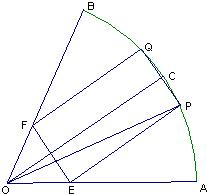 如图,在半径为R、圆心角为
如图,在半径为R、圆心角为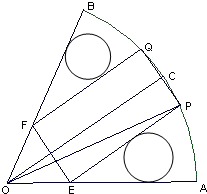 如图,在半径为R、圆心角为
如图,在半径为R、圆心角为 (2011•成都二模)如图,在半径为l的球O中.AB、CD是两条互相垂直的直径,半径OP⊥平面ABCD.点E、F分别为大圆上的劣弧
(2011•成都二模)如图,在半径为l的球O中.AB、CD是两条互相垂直的直径,半径OP⊥平面ABCD.点E、F分别为大圆上的劣弧
 、
、 、
、 三点,
三点, ,球心
,球心 到平面
到平面 距离是
距离是 ,则
,则 B.
B.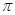
 D.2
D.2