题目内容
若－
≤x≤0，求arcsin(cosx)－arccos(sinx)的值
答案：
解析：
解析：
|
解∵－ |
≤x≤0，∴0≤cosx≤1，－1≤sinx≤0．令α＝arcsin(cosx)，则0≤α≤
|sinx|＝－sinx．再令β＝arccos(sinx)，则β∈[
，π]，∴cosβ＝sinx，sinβ＝
|cosx|＝cosx．又0≤α≤
，－π≤－β≤-
练习册系列答案
相关题目
(x≠0，常数a
R)．
上为增函数，求实数a的取值范围．
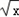，g（x）=alnx，a
R．
的解析式；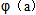
，证明：当a
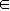（0，+
）时，
1
)(x+a)(a
R).(1)若函数f(x)的图象上有与x轴平行的切线，求a的范围；(2)若
(-1)=0,(I)求函数f(x)的单调区间；（II）证明对任意的x1、x2
恒成立.
，g（x）=alnx，a
R。
（a）的解析式；
）时， 
1.
，g（x）=alnx，a
R。
（a）的解析式；
）时， 
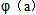
1.