题目内容
已知函数f(x)=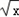 ,g(x)=alnx,a
,g(x)=alnx,a R.
R.
(1)若曲线y=f(x)与曲线y=g(x)相交,且在交点处有相同的切线,求a的值及该切线的方程;
(2)设函数h(x)=f(x)﹣g(x),当h(x)存在最小值时,求其最小值 的解析式;
的解析式;
(3)对(2)中的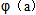 ,证明:当a
,证明:当a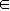 (0,+
(0,+ )时,
)时,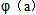
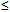 1
1
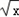 ,g(x)=alnx,a
,g(x)=alnx,a R.
R.(1)若曲线y=f(x)与曲线y=g(x)相交,且在交点处有相同的切线,求a的值及该切线的方程;
(2)设函数h(x)=f(x)﹣g(x),当h(x)存在最小值时,求其最小值
 的解析式;
的解析式;(3)对(2)中的
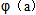 ,证明:当a
,证明:当a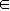 (0,+
(0,+ )时,
)时,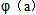
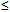 1
1解:(1) 函数f(x)=
函数f(x)= ,g(x)=alnx,a
,g(x)=alnx,a R.
R.
f '(x)=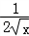 ,g '(x)=
,g '(x)= (x>0),
(x>0),
由已知得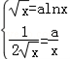 解得
解得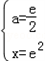
 两条曲线交点的坐标为(e2,e).
两条曲线交点的坐标为(e2,e).
切线的斜率为k=f '(e2)= ,
,
 切线的方程为y﹣e=
切线的方程为y﹣e= (x﹣e2).
(x﹣e2).
(2)由条件知h(x)= ﹣alnx(x>0),
﹣alnx(x>0),
 h '(x)=
h '(x)= ﹣
﹣ =
= ,
,
①当a>0时,令h '(x)=0,解得x=4a2.
 当0<x<4a2时,h '(x)<0,h(x)在(0,4a2)上单调递减;
当0<x<4a2时,h '(x)<0,h(x)在(0,4a2)上单调递减;
当x>4a2时,h '(x)>0,h(x)在(4a2,+ )上单调递增.
)上单调递增.
 x=4a2是h(x)在(0,+
x=4a2是h(x)在(0,+ )上的惟一极值点,且是极小值点,从而也是h(x)的最小值点.
)上的惟一极值点,且是极小值点,从而也是h(x)的最小值点.
 最小值
最小值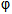 (a)=h(4a2)=2a﹣aln(4a2)=2a[1﹣ln (2a)].
(a)=h(4a2)=2a﹣aln(4a2)=2a[1﹣ln (2a)].
②当a 0时,h '(x)=
0时,h '(x)= >0,h(x)在(0,+
>0,h(x)在(0,+ )上单调递增,无最小值.
)上单调递增,无最小值.
故h(x)的最小值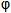 (a)的解析式为
(a)的解析式为 (a)=2a[1﹣ln (2a)](a>0).
(a)=2a[1﹣ln (2a)](a>0).
(3)证明:由(2)知 (a)=2a(1﹣ln 2﹣ln a),
(a)=2a(1﹣ln 2﹣ln a),
则 '(a)=﹣2ln (2a).
'(a)=﹣2ln (2a).
令 '(a)=0,解得a=
'(a)=0,解得a= .
.
当0<a< 时,
时, '(a)>0,
'(a)>0,
 (a)在(0,
(a)在(0, )上单调递增;
)上单调递增;
当a> 时,
时, '(a)<0,
'(a)<0,
 (a)在(
(a)在( ,+
,+ )上单调递减.
)上单调递减.

 (a)在a=
(a)在a= 处取得极大值?(
处取得极大值?( )=1.
)=1.

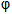 (a)在(0,+
(a)在(0,+ )上有且只有一个极值点,
)上有且只有一个极值点,

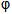 (
( )=1也是
)=1也是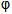 (a)的最大值.
(a)的最大值.
 当a
当a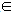 (0,+
(0,+ )时,总有
)时,总有 (a)
(a) 1.
1.
 函数f(x)=
函数f(x)= ,g(x)=alnx,a
,g(x)=alnx,a R.
R.f '(x)=
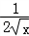 ,g '(x)=
,g '(x)= (x>0),
(x>0),由已知得
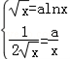 解得
解得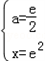
 两条曲线交点的坐标为(e2,e).
两条曲线交点的坐标为(e2,e).切线的斜率为k=f '(e2)=
 ,
, 切线的方程为y﹣e=
切线的方程为y﹣e= (x﹣e2).
(x﹣e2).(2)由条件知h(x)=
 ﹣alnx(x>0),
﹣alnx(x>0), h '(x)=
h '(x)= ﹣
﹣ =
= ,
,①当a>0时,令h '(x)=0,解得x=4a2.
 当0<x<4a2时,h '(x)<0,h(x)在(0,4a2)上单调递减;
当0<x<4a2时,h '(x)<0,h(x)在(0,4a2)上单调递减;当x>4a2时,h '(x)>0,h(x)在(4a2,+
 )上单调递增.
)上单调递增. x=4a2是h(x)在(0,+
x=4a2是h(x)在(0,+ )上的惟一极值点,且是极小值点,从而也是h(x)的最小值点.
)上的惟一极值点,且是极小值点,从而也是h(x)的最小值点. 最小值
最小值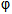 (a)=h(4a2)=2a﹣aln(4a2)=2a[1﹣ln (2a)].
(a)=h(4a2)=2a﹣aln(4a2)=2a[1﹣ln (2a)].②当a
 0时,h '(x)=
0时,h '(x)= >0,h(x)在(0,+
>0,h(x)在(0,+ )上单调递增,无最小值.
)上单调递增,无最小值.故h(x)的最小值
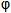 (a)的解析式为
(a)的解析式为 (a)=2a[1﹣ln (2a)](a>0).
(a)=2a[1﹣ln (2a)](a>0).(3)证明:由(2)知
 (a)=2a(1﹣ln 2﹣ln a),
(a)=2a(1﹣ln 2﹣ln a),则
 '(a)=﹣2ln (2a).
'(a)=﹣2ln (2a).令
 '(a)=0,解得a=
'(a)=0,解得a= .
.当0<a<
 时,
时, '(a)>0,
'(a)>0,
 (a)在(0,
(a)在(0, )上单调递增;
)上单调递增;当a>
 时,
时, '(a)<0,
'(a)<0,
 (a)在(
(a)在( ,+
,+ )上单调递减.
)上单调递减.
 (a)在a=
(a)在a= 处取得极大值?(
处取得极大值?( )=1.
)=1.
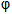 (a)在(0,+
(a)在(0,+ )上有且只有一个极值点,
)上有且只有一个极值点,
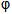 (
( )=1也是
)=1也是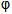 (a)的最大值.
(a)的最大值. 当a
当a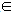 (0,+
(0,+ )时,总有
)时,总有 (a)
(a) 1.
1.
练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|