题目内容
设函数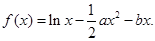
(1)若x=1是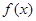 的极大值点,求a的取值范围。
的极大值点,求a的取值范围。
(2)当a=0,b=-1时,函数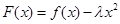 有唯一零点,求正数
有唯一零点,求正数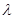 的值。
的值。
(Ⅰ) 的定义域为
的定义域为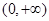 ,
,
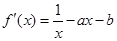 ,由
,由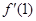 =0,得
=0,得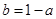 .
.
∴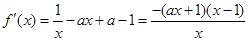 .
.
①若a≥0,由 =0,得x=1.
=0,得x=1.
当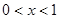 时,
时,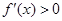 ,此时
,此时 单调递增;
单调递增;
当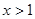 时,
时,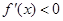 ,此时
,此时 单调递减.所以x=1是
单调递减.所以x=1是 的极大值点.
的极大值点.
②若a<0,由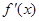 =0,得x=1,或x=
=0,得x=1,或x= .
.
因为x=1是 的极大值点,所以
的极大值点,所以 >1,解得-1<a<0.[来
>1,解得-1<a<0.[来
综合①②:a的取值范围是a>-1.
(Ⅱ)因为函数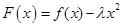 有唯一零点,即
有唯一零点,即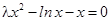 有唯一实数解,
有唯一实数解,
设 ,则
,则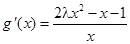 .令
.令 ,
, .
.
因为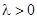 ,所以△=
,所以△= >0,方程有两异号根设为x1<0,x2>0.因为x>0,所以x1应舍去.
>0,方程有两异号根设为x1<0,x2>0.因为x>0,所以x1应舍去.
当 时,
时,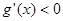 ,
,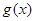 在(0,
在(0, )上单调递减;
)上单调递减;
当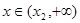 时,
时, ,
,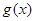 在(
在( ,+∞)单调递增.
,+∞)单调递增.
当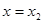 时,
时,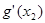 =0,
=0,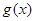 取最小值
取最小值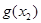 .
.
因为 有唯一解,所以
有唯一解,所以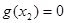 ,
,
则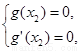 即
即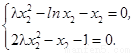
因为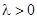 ,所以
,所以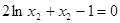 (*)
(*)
设函数 ,因为当
,因为当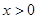 时,
时,
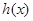 是增函数,所以
是增函数,所以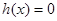 至多有一解.
至多有一解.
因为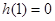 ,所以方程(*)的解为
,所以方程(*)的解为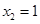 ,
,
代入方程组解得
【解析】略

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案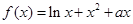 .
. 时,
时,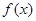 取得极值,求
取得极值,求 的值;
的值; ,当
,当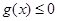 在其定义域内恒成立,并证明
在其定义域内恒成立,并证明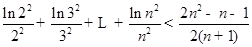 (
(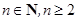 ).
).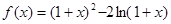
 在
在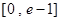 有实数解,求实数m的取值范围;
有实数解,求实数m的取值范围;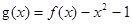 ,若关于x的方程
,若关于x的方程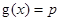 至少有一个解,求p 的最小值.
至少有一个解,求p 的最小值.
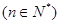
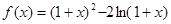
 在
在 有实数解,求实数m的取值范围;
有实数解,求实数m的取值范围; ,若关于x的方程
,若关于x的方程 至少有一个解,求p 的最小值.
至少有一个解,求p 的最小值.
