题目内容
已知函数
(1)当k=1时,求函数f(x)的极值
(2)当k>0时,若函数f(x)在区间[-3,1]上单调递减,求实数k的取值范围.
【答案】分析:(1)先求函数的导数,再令导数等于0,求出极值点,判断极值点左右两侧导数的正负,当左正右负时有极大值,当左负右正时有极小值.再代入原函数求出极大值和极小值.
(2)因为当k>0时,若函数f(x)在区间[-3,1]上单调递减,所以k>0时,在区间[-3,1]上,f′(x)<0恒成立,而f′(x)是关于x的二次函数,结合函数的对称轴与定义域,即可求出参数k的取值范围.
解答:解:(1)f′(x)=kx2+2x-3,当k=1时, ,f′(x)=x2+2x-3,
,f′(x)=x2+2x-3,
令f′(x)=0,即x2+2x-3=0,解得,x=-3或x=1
且当x>1时,f′(x)>0.当-3<x<1时,f′(x)<0.当x<-3时,f′(x)>0.
∴当x=-3时,函数f(x)有极大值为f(-3)=10,当x=1时,函数f(x)有极小值为f(1)=
(2)∵当k>0时,若函数f(x)在区间[-3,1]上单调递减,∴k>0时,在区间[-3,1]上,f′(x)<0恒成立.
即k>0时,在区间[-3,1]上,kx2+2x-3<0恒成立,
函数f′(x)=kx2+2x-3是关于x的二次函数,且对称轴x=- ,∵k>0,∴-
,∵k>0,∴- <0
<0
当- ≤-3,即0<k≤
≤-3,即0<k≤ 时,只需f′(-3)<0,即9k-9<0,解得k<1∴0<k≤
时,只需f′(-3)<0,即9k-9<0,解得k<1∴0<k≤ 时满足条件
时满足条件
当- >-3,即k>
>-3,即k> 时,只需f′(-
时,只需f′(- )<0,即
)<0,即 0,解得,-
0,解得,- <k<0,∵k>0,∴不成立
<k<0,∵k>0,∴不成立
∴实数k的取值范围0<k≤ .
.
点评:本题主要考查函数的导数与极值,单调区间的关系,以及恒成立问题求参数的取值范围,属于导数的应用.
(2)因为当k>0时,若函数f(x)在区间[-3,1]上单调递减,所以k>0时,在区间[-3,1]上,f′(x)<0恒成立,而f′(x)是关于x的二次函数,结合函数的对称轴与定义域,即可求出参数k的取值范围.
解答:解:(1)f′(x)=kx2+2x-3,当k=1时,
 ,f′(x)=x2+2x-3,
,f′(x)=x2+2x-3,令f′(x)=0,即x2+2x-3=0,解得,x=-3或x=1
且当x>1时,f′(x)>0.当-3<x<1时,f′(x)<0.当x<-3时,f′(x)>0.
∴当x=-3时,函数f(x)有极大值为f(-3)=10,当x=1时,函数f(x)有极小值为f(1)=

(2)∵当k>0时,若函数f(x)在区间[-3,1]上单调递减,∴k>0时,在区间[-3,1]上,f′(x)<0恒成立.
即k>0时,在区间[-3,1]上,kx2+2x-3<0恒成立,
函数f′(x)=kx2+2x-3是关于x的二次函数,且对称轴x=-
 ,∵k>0,∴-
,∵k>0,∴- <0
<0当-
 ≤-3,即0<k≤
≤-3,即0<k≤ 时,只需f′(-3)<0,即9k-9<0,解得k<1∴0<k≤
时,只需f′(-3)<0,即9k-9<0,解得k<1∴0<k≤ 时满足条件
时满足条件当-
 >-3,即k>
>-3,即k> 时,只需f′(-
时,只需f′(- )<0,即
)<0,即 0,解得,-
0,解得,- <k<0,∵k>0,∴不成立
<k<0,∵k>0,∴不成立∴实数k的取值范围0<k≤
 .
.点评:本题主要考查函数的导数与极值,单调区间的关系,以及恒成立问题求参数的取值范围,属于导数的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 与4的大小.
与4的大小.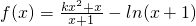 .
. .
.