题目内容
已知函数
(1)当x∈[1,+∞)时,判断f(x)的单调性并证明;
(2)设函数g(x)=x•f(x)+|x2-1|+(k-a)x-a,k为常数..若关于x的方程g(x)=0在(0,2)上有两个解x1,x2,求k的取值范围,并比较 与4的大小.
与4的大小.
解:(1)∵函数 =
=
任取1≤x1<x2,
∴x1-x2<0,x1•x2>1,
又∵a<1
得x1•x2-a>0
则f(x1)-f(x2)=( )-(
)-( )=
)= =
= <0
<0
即f(x1)<f(x2)
故函数f(x)在[1,+∞)上单调递增
(2)函数g(x)=x•f(x)+|x2-1|+(k-a)x-a=x2+kx+|x2-1|= ,
,
故函数g(x)在(0,1]上是单调函数,故方程g(x)=0在(0,1]上到多一个解
方程g(x)=0在(0,2)上有两个解x1,x2,不妨设0<x1<x2<2
若1<x1<x2<2,则x1•x2= <0,不符合题意,
<0,不符合题意,
∴0<x1≤1<x2<2,
由g(x1)=0得:k=- ,故k≤-1;
,故k≤-1;
由g(x2)=0得:k= -2x2,故
-2x2,故 <k<-1
<k<-1
综上当 <k<-1时,方程g(x)=0在(0,2)上有两个解
<k<-1时,方程g(x)=0在(0,2)上有两个解
∵0<x1≤1<x2<2,
∴k=- ,2x22+kx2-1=0
,2x22+kx2-1=0
消去k得,2x1x22-x1-x2=0
即 +
+ =2x2,
=2x2,
∵x2<2
∴ <4
<4
分析:(1)任取1≤x1<x2,根据实数的性质,判断f(x1)-f(x2)的符号,进而判断f(x1)与f(x2)的大小关系,进而根据函数单调性的定义,可得答案.
(2)利用零点分段法,可将函数g(x)的解析式化为分段函数的形式,结合函数的单调性,及二次函数的图象和性质,可得0<x1≤1<x2<2,进而求出k的取值范围,及 与4的大小.
与4的大小.
点评:本题考查的知识点是函数单调性的判断与证明,不等关系与不等式,其中熟练掌握单调性的证明过程判断出函数的单调性是解答的关键.
 =
=
任取1≤x1<x2,
∴x1-x2<0,x1•x2>1,
又∵a<1
得x1•x2-a>0
则f(x1)-f(x2)=(
 )-(
)-( )=
)= =
= <0
<0即f(x1)<f(x2)
故函数f(x)在[1,+∞)上单调递增
(2)函数g(x)=x•f(x)+|x2-1|+(k-a)x-a=x2+kx+|x2-1|=
 ,
,故函数g(x)在(0,1]上是单调函数,故方程g(x)=0在(0,1]上到多一个解
方程g(x)=0在(0,2)上有两个解x1,x2,不妨设0<x1<x2<2
若1<x1<x2<2,则x1•x2=
 <0,不符合题意,
<0,不符合题意,∴0<x1≤1<x2<2,
由g(x1)=0得:k=-
 ,故k≤-1;
,故k≤-1;由g(x2)=0得:k=
 -2x2,故
-2x2,故 <k<-1
<k<-1综上当
 <k<-1时,方程g(x)=0在(0,2)上有两个解
<k<-1时,方程g(x)=0在(0,2)上有两个解∵0<x1≤1<x2<2,
∴k=-
 ,2x22+kx2-1=0
,2x22+kx2-1=0消去k得,2x1x22-x1-x2=0
即
 +
+ =2x2,
=2x2,∵x2<2
∴
 <4
<4分析:(1)任取1≤x1<x2,根据实数的性质,判断f(x1)-f(x2)的符号,进而判断f(x1)与f(x2)的大小关系,进而根据函数单调性的定义,可得答案.
(2)利用零点分段法,可将函数g(x)的解析式化为分段函数的形式,结合函数的单调性,及二次函数的图象和性质,可得0<x1≤1<x2<2,进而求出k的取值范围,及
 与4的大小.
与4的大小.点评:本题考查的知识点是函数单调性的判断与证明,不等关系与不等式,其中熟练掌握单调性的证明过程判断出函数的单调性是解答的关键.

练习册系列答案
相关题目

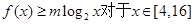 恒成立,求m的取值范围
恒成立,求m的取值范围
 恒成立,求m的取值范围.
恒成立,求m的取值范围.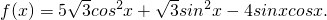
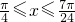 ,求f(x)的单调区间.
,求f(x)的单调区间.
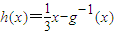 在区间(e,3)内无零点,在区间(3,e2)内有且只有一个零点;
在区间(e,3)内无零点,在区间(3,e2)内有且只有一个零点;
 ,求f(x)的单调区间.
,求f(x)的单调区间.