题目内容

sin(π-α)cos(
π
2
+α)
sin(π+α)
+
sin(
π
2
-α)cos(
π
2
-α)
cos(π+α)
=
0
0
．
分析：原式第一项分子的第一个因式利用诱导公式sin（π-α）=sinα化简，第二个因式利用诱导公式cos（
π
2
+α）=-sinα化简，分母利用诱导公式sin（π+α）=-sinα化简，第二项分子第一个因式利用诱导公式sin（
π
2
-α）=cosα，第二个因式利用cos（
π
2
-α）=sinα化简，分母利用诱导公式cos（π+α）=-cosα化简，约分后合并即可得到值．
解答：解：原式=
sinα•(-sinα)
-sinα
+
cosαsinα
-cosα

=
-sin2α
-sinα
+
cosαsinα
-cosα

=sinα-sinα=0．
故答案为：0
点评：此题考查了运用诱导公式化简求值，熟练掌握诱导公式是解本题的关键．
练习册系列答案
相关题目
在（0，2π）内使 sin x＞|co s x|的x的取值范围是（　　）
A、(
1
4
π，
3
4
π)
B、(
1
4
π，
1
2
π]∪(
5
4
π，
3
2
π]
C、(
1
4
π，
1
2
π)
D、(
5
4
π，
7
4
π)
已知coα=-
513
，α为第三象限角，求sinα，tanα的值．
在A、B、C、D四小题中只能选做2题，每小题10分，共计20分．解答应写出文字说明、证明过程或演算步骤．
A．选修4-1：几何证明选讲
如图，CP是圆O的切线，P为切点，直线CO交圆O于A，B两点，AD⊥CP，垂足为D．
求证：∠DAP=∠BAP．
B．选修4-2：矩阵与变换
设a＞0，b＞0，若矩阵A=
.
a0
0b
.
把圆C：x2+y2=1变换为椭圆E：
x2
4
+
y2
3
=1．
（1）求a，b的值；（2）求矩阵A的逆矩阵A-1
C．选修4-4：坐标系与参数方程在极坐标系中，已知圆C：ρ=4cosθ被直线l：ρsin（θ-\frac{π}{6}）=a截得的弦长为2
3
求实数a的值．
D．选修4-5：不等式选讲已知a，b是正数，求证：a2+4b2+
1
ab
≥4．
在（0，2π）内使 sin x＞|co s x|的x的取值范围是（　　）
A．(
1
4
π，
3
4
π)		B．(
1
4
π，
1
2
π]∪(
5
4
π，
3
2
π]
C．(
1
4
π，
1
2
π)		D．(
5
4
π，
7
4
π)
在A、B、C、D四小题中只能选做2题，每小题10分，共计20分．解答应写出文字说明、证明过程或演算步骤．
A．选修4-1：几何证明选讲
如图，CP是圆O的切线，P为切点，直线CO交圆O于A，B两点，AD⊥CP，垂足为D．
求证：∠DAP=∠BAP．
B．选修4-2：矩阵与变换
设a＞0，b＞0，若矩阵A=把圆C：x2+y2=1变换为椭圆E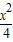：=1．
（1）求a，b的值；（2）求矩阵A的逆矩阵A-1
C．选修4-4：坐标系与参数方程在极坐标系中，已知圆C：ρ=4cosθ被直线l：ρsin（θ-\frac{π}{6}）=a截得的弦长为2求实数a的值．
D．选修4-5：不等式选讲已知a，b是正数，求证：a2+4b2≥4．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网