题目内容

若一个三棱锥中有一条棱长为x（其中(0＜x＜
3
)），其余各条棱长均为1，则它的体积
 
．（用x表示）
分析：由题意画出三棱锥的图形，取BC，AD的中点分别为E，F，求出AED的面积，然后求出棱锥的体积．
解答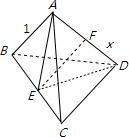：精英家教网解：由题意画出棱锥的图形，AB=BC=CD=BD=AC=1，AD=x；
取BC，AD的中点分别为E，F，
可知平面AED垂直BC，S△AED=
1
2
AD•EF
EF=
(
3
2
)2-(
x
2
)2

所以V(x)=
1
3
•S△AED•BC=
1
12
x
3-x2

故答案为：V(x)=
1
12
x
3-x2
  (0＜x＜
3
)
点评：本题是基础题，考查空间想象能力，计算能力，本题的关键是棱锥的转化为两个棱锥，底面AED的处理是解题的关键．
练习册系列答案
相关题目
若一个三棱锥中有一条棱长为x（其中0＜x＜
3
），其余各条棱长均为1，则它的表面积S（x）=
1
2
(x
4-x
+
3
)
1
2
(x
4-x
+
3
)
．（用x表示）
若一个三棱锥中有一条棱长为x（其中），其余各条棱长均为1，则它的体积     ．（用x表示）
若一个三棱锥中有一条棱长为x（其中），其余各条棱长均为1，则它的体积     ．（用x表示）
若一个三棱锥中有一条棱长为x（其中），其余各条棱长均为1，则它的体积     ．（用x表示）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网