题目内容
如图,A为椭圆
+
=1(a>b>0)上的一个动点,弦AB,AC分别过焦点F1,F2.当AC垂直于x轴时,恰好|AF1|:|AF2|=3:1.
(1)求该椭圆的离心率;
(2)设
=λ1
,
=λ2
,试判断λ1+λ2是否为定值?若是,则求出该定值;若不是,请说明理由.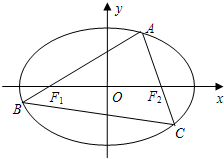
| x2 |
| a2 |
| y2 |
| b2 |
(1)求该椭圆的离心率;
(2)设
| AF1 |
| F1B |
| AF2 |
| F2C |

(1)当AC垂直于x轴时,|AF1|:|AF2|=3:1,由|AF1|+|AF2|=2a,
得|AF1|=
,|AF2|=
在Rt△AF1F2中,|AF1|2=|AF2|2+(2c)2
解得 e=
.…(5分)
(2)由e=
,则
=
=
=
,b=c.
焦点坐标为F1(-b,0),F2(b,0),则椭圆方程为
+
=1,
化简有x2+2y2=2b2.
设A(x0,y0),B(x1,y1),C(x2,y2),
①若直线AC⊥x轴,x0=b,λ2=1,λ1=
=5
∴λ1+λ2=6. …(8分)
②若直线AC的斜率存在,则直线AC方程为y=
(x-b)
代入椭圆方程有(3b2-2bx0)y2+2by0(x0-b)y-b2y02=0.
由韦达定理得:y0y2=-
,∴y2=-
…(10分)
所以λ2=
=
=
,
同理可得λ1=
=
…(12分)
故λ1+λ2=
=6.综上所述:λ1+λ2是定值6.…(14分)
得|AF1|=
| 3a |
| 2 |
| a |
| 2 |
解得 e=
| ||
| 2 |
(2)由e=
| ||
| 2 |
| b |
| a |
| ||
| a |
| 1-e2 |
| ||
| 2 |
焦点坐标为F1(-b,0),F2(b,0),则椭圆方程为
| x2 |
| 2b2 |
| y2 |
| b2 |
化简有x2+2y2=2b2.
设A(x0,y0),B(x1,y1),C(x2,y2),
①若直线AC⊥x轴,x0=b,λ2=1,λ1=
| 3b+2b |
| b |
∴λ1+λ2=6. …(8分)
②若直线AC的斜率存在,则直线AC方程为y=
| y0 |
| x0-b |
代入椭圆方程有(3b2-2bx0)y2+2by0(x0-b)y-b2y02=0.
由韦达定理得:y0y2=-
| b2y02 |
| 3b2-2bx0 |
| b2y0 |
| 3b2-2bx0 |
所以λ2=
| |AF2| |
| |F2C| |
| y0 |
| -y2 |
| 3b-2x0 |
| b |
同理可得λ1=
| -3b-2x0 |
| -b |
| 3b+2x0 |
| b |
故λ1+λ2=
| 6b |
| b |

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
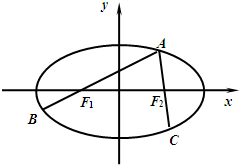 如图,A为椭圆
如图,A为椭圆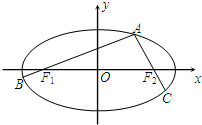 如图,A为椭圆
如图,A为椭圆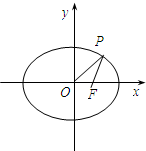 如图,F为椭圆
如图,F为椭圆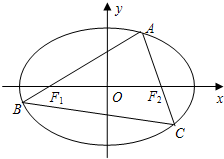 如图,A为椭圆
如图,A为椭圆