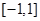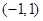题目内容
设函数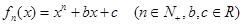
(1)设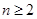 ,
,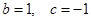 ,证明:
,证明: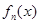 在区间
在区间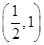 内存在唯一的零点;
内存在唯一的零点;
(2)设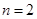 ,若对任意
,若对任意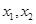
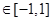 ,有
,有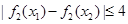 ,求
,求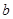 的取值范围;
的取值范围;
(3)在(1)的条件下,设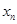 是
是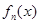 在
在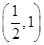 内的零点,判断数列
内的零点,判断数列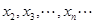 的增减性。
的增减性。
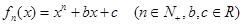
(1)设
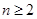 ,
,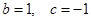 ,证明:
,证明: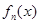 在区间
在区间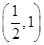 内存在唯一的零点;
内存在唯一的零点;(2)设
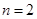 ,若对任意
,若对任意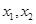
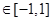 ,有
,有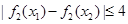 ,求
,求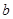 的取值范围;
的取值范围;(3)在(1)的条件下,设
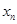 是
是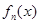 在
在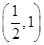 内的零点,判断数列
内的零点,判断数列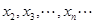 的增减性。
的增减性。见解析



【考点定位】本题主要考察函数与方程,导数的综合应用,函数与数列的综合,考查综合能力

练习册系列答案
相关题目
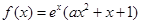 ,且曲线y=f(x)在x=1处的切线与x轴平行。
,且曲线y=f(x)在x=1处的切线与x轴平行。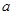 的值,并讨论
的值,并讨论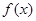 的单调性;
的单调性;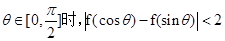
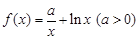 .
.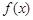 在
在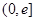 上的单调性(
上的单调性(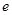 为自然对数的底);
为自然对数的底);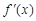 为
为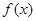 的导函数,若函数
的导函数,若函数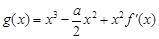 在区间
在区间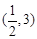 上存在极值,求实数
上存在极值,求实数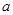 的取值范围。
的取值范围。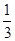 x3-(1+a)x2+4ax+24a,其中常数a>1.
x3-(1+a)x2+4ax+24a,其中常数a>1. 有极值,则导函数
有极值,则导函数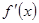 的图象不可能是 ( )
的图象不可能是 ( )
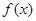 对任意x都有
对任意x都有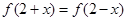 ,且其导函数
,且其导函数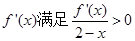 ,则当
,则当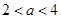 ,有 ( )
,有 ( )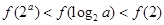
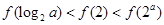

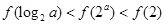
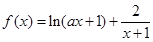 ,其中
,其中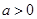 .
.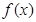 在
在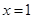 处取得极值,求曲线
处取得极值,求曲线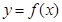 在点
在点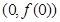 处的切线方程;
处的切线方程;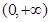 的单调性;
的单调性;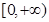 上的最小值为2,求
上的最小值为2,求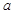 的取值范围.
的取值范围.
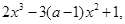 其中
其中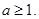
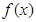 的单调区间;
的单调区间;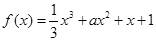 在
在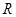 上无极值点,则实数
上无极值点,则实数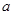 的取值范围是( )
的取值范围是( )