题目内容
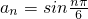 ,则a1+a2+a3+…+a2010=________.
,则a1+a2+a3+…+a2010=________.
2+
分析:根据正弦函数y=sinx是周期为2π的周期函数,得出对于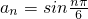 ,其值呈周期性变化,T=2π,且一个周期内的函数值之和为0,利用周期性得出a1+a2+a3+…+a2010=a1+a2+a3+…+a6,从而求出其值.
,其值呈周期性变化,T=2π,且一个周期内的函数值之和为0,利用周期性得出a1+a2+a3+…+a2010=a1+a2+a3+…+a6,从而求出其值.
解答:由于正弦函数y=sinx是周期为2π的周期函数,
∴对于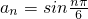 ,其值呈周期性变化,T=2π,且一个周期内的函数值之和为0
,其值呈周期性变化,T=2π,且一个周期内的函数值之和为0
∵2010=167×12+6
∴a1+a2+a3+…+a2010=a1+a2+a3+…+a6= +
+ +
+ +
+ +
+ +
+
=2+ .
.
故答案为:2+ .
.
点评:本小题主要考查正弦函数的函数值、三角函数的周期性及其求法等基础知识,考查运算求解能力,考查转化思想.属于基础题.

分析:根据正弦函数y=sinx是周期为2π的周期函数,得出对于
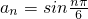 ,其值呈周期性变化,T=2π,且一个周期内的函数值之和为0,利用周期性得出a1+a2+a3+…+a2010=a1+a2+a3+…+a6,从而求出其值.
,其值呈周期性变化,T=2π,且一个周期内的函数值之和为0,利用周期性得出a1+a2+a3+…+a2010=a1+a2+a3+…+a6,从而求出其值.解答:由于正弦函数y=sinx是周期为2π的周期函数,
∴对于
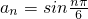 ,其值呈周期性变化,T=2π,且一个周期内的函数值之和为0
,其值呈周期性变化,T=2π,且一个周期内的函数值之和为0∵2010=167×12+6
∴a1+a2+a3+…+a2010=a1+a2+a3+…+a6=
 +
+ +
+ +
+ +
+ +
+
=2+
 .
.故答案为:2+
 .
.点评:本小题主要考查正弦函数的函数值、三角函数的周期性及其求法等基础知识,考查运算求解能力,考查转化思想.属于基础题.

练习册系列答案
相关题目
已知函数f(x)=
,an=
,则a1?a2?a3?…?a9=( )
|
| f(n) |
| f(n+1) |
A、
| ||
B、-
| ||
C、
| ||
D、-
|