题目内容
13．已知i是虚数单位，若复数z=$\frac{3+4i}{i}$，则z的共轭复数$\overline{z}$的虚部为（ ）| A． | -3i | B． | -3 | C． | 3i | D． | 3 |
分析 利用复数的运算法则、共轭复数的定义、虚部的定义即可得出．
解答 解：复数z=$\frac{3+4i}{i}$=$\frac{-i（3+4i）}{-i•i}$=4-3i，则z的共轭复数$\overline{z}$=4+3i的虚部为3．
故选：D．
点评 本题考查了复数的运算法则、共轭复数的定义、虚部的定义，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
3．双曲线$\frac{y^2}{3}-{x^2}=1$的焦点坐标是（ ）
| A． | $（±\sqrt{2}，0）$ | B． | $（0，±\sqrt{2}）$ | C． | （0，±2） | D． | （±2，0） |
1．已知集合M={x|x2-x-2=0}，N={-1，0}，则M∩N=（ ）
| A． | {-1，0，2} | B． | {-1} | C． | {0} | D． | ∅ |
已知椭圆C；$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞c）的左、右焦点分别为F1（-c，0）、F2（c，0），过原点O的直线（与x轴不重合）与椭圆C相交于D、Q两点，且|DF1|+|QF1|=4，P为椭圆C上的动点，△PF1F2的面积的最大值为$\sqrt{3}$．
3．
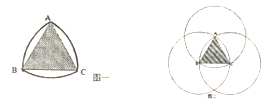如图一所示，由弧AB，弧AC，弧BC所组成的图形叫做勒洛三角形，它由德国机械工程专家、机械运动学家勒洛首先发现的，它的构成如图二所示，以正三角形ABCd的每个顶点为圆心，以边长为半径，在另两个顶点间作一段弧，由三段弧所围成的曲边三角形即为勒洛三角形，有一个如图一所示的靶子，某人向靶子射出一箭，若此箭一定能射中靶子且射中靶子中的任意一点是等可能的，则此箭恰好射中三角形ABC内部（即阴影部分）的概率为（ ）
如图一所示，由弧AB，弧AC，弧BC所组成的图形叫做勒洛三角形，它由德国机械工程专家、机械运动学家勒洛首先发现的，它的构成如图二所示，以正三角形ABCd的每个顶点为圆心，以边长为半径，在另两个顶点间作一段弧，由三段弧所围成的曲边三角形即为勒洛三角形，有一个如图一所示的靶子，某人向靶子射出一箭，若此箭一定能射中靶子且射中靶子中的任意一点是等可能的，则此箭恰好射中三角形ABC内部（即阴影部分）的概率为（ ）| A． | $\frac{\sqrt{3}}{2π-\sqrt{3}}$ | B． | $\frac{\sqrt{3}}{2（π-\sqrt{3}}）$ | C． | $\frac{2π-3\sqrt{3}}{2（π-\sqrt{3}）}$ | D． | $\frac{2π-2\sqrt{3}}{2π-\sqrt{3}}$ |