题目内容
18.在△ABC中,D为线段BC上一点(不能与端点重合),∠ACB=$\frac{π}{3},AB=\sqrt{7}$,AC=3,BD=1,则AD=$\sqrt{7}$.分析 由已知利用余弦定理可求BC的值,进而可求DC的值,再次利用余弦定理即可求得AD的值.
解答 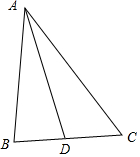 解:在△ABC中,∵∠ACB=$\frac{π}{3},AB=\sqrt{7}$,AC=3,
解:在△ABC中,∵∠ACB=$\frac{π}{3},AB=\sqrt{7}$,AC=3,
∴由余弦定理AB2=AC2+BC2-2AC•BC•sin∠ACB,可得:7=9+BC2-2×3×BC×$\frac{1}{2}$,整理可得:BC2-3BC+2=0,
∴解得:BC=2或1,
∵D为线段BC上一点(不能与端点重合),可知,BC≠1,
∴BC=2,CD=BC-BD=2-1=1,
∴由余弦定理可得:AD=$\sqrt{A{C}^{2}+C{D}^{2}-2AC•CD•cos∠ACB}$=$\sqrt{9+1-2×3×1×\frac{1}{2}}$=$\sqrt{7}$.
故答案为:$\sqrt{7}$.
点评 本题主要考查了余弦定理在解三角形中的应用,考查了计算能力和转化思想,属于基础题.

练习册系列答案
相关题目
6.已知θ∈(0,π),tanθ=-$\frac{5}{12}$,则cosθ=( )
| A. | $\frac{12}{13}$ | B. | $-\frac{12}{13}$ | C. | $-\frac{5}{13}$ | D. | $\frac{5}{13}$ |
13.设集合M={x|1<x<5},N={0,2,3,5},则M∩N=( )
| A. | {x|2<x<4} | B. | {0,2,3} | C. | {2,3} | D. | {x|2<x<3} |
17.设公比为q(q≠1)的等比数列{an}的前n项和为Sn,且Sn=qn+k,那么k等于( )
| A. | 2 | B. | 1 | C. | 0 | D. | -1 |