题目内容
已知椭圆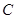 的两个焦点为
的两个焦点为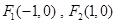 ,点
,点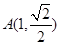 在椭圆
在椭圆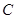 上.
上.
(Ⅰ)求椭圆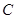 的方程;
的方程;
(Ⅱ)已知点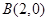 ,设点
,设点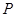 是椭圆
是椭圆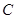 上任一点,求
上任一点,求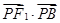 的取值范围.
的取值范围.
 的两个焦点为
的两个焦点为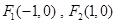 ,点
,点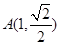 在椭圆
在椭圆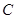 上.
上.(Ⅰ)求椭圆
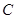 的方程;
的方程;(Ⅱ)已知点
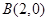 ,设点
,设点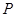 是椭圆
是椭圆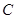 上任一点,求
上任一点,求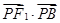 的取值范围.
的取值范围.(1) (2)
(2)
 (2)
(2)
试题分析:解:(1)设椭圆
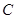 的方程为
的方程为 1分
1分由椭圆定义,
 3分
3分∴

 . 5分
. 5分故所求的椭圆方程为
 . 6分
. 6分(2)设
 7分
7分∴
 9分
9分∵点
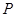 在椭圆上,∴
在椭圆上,∴ 10
10∴

∵
 12分
12分∴

 有最小值
有最小值 ;
; ,
, 有最大值
有最大值
∴
 ,∴
,∴ 的范围是
的范围是 14分
14分点评:主要是考查了直线与椭圆的位置关系,以及向量的数量积的运用,属于基础题。

练习册系列答案
相关题目
 的左、右焦点分别为F1(-1,0),F2(1,0),过F1作与x轴不重合的直线l交椭圆于A,B两点.
的左、右焦点分别为F1(-1,0),F2(1,0),过F1作与x轴不重合的直线l交椭圆于A,B两点.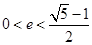 ,
,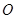 为坐标原点,求证:
为坐标原点,求证: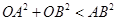 .
.
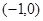 、
、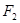
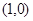 为椭圆的焦点,且直线
为椭圆的焦点,且直线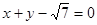 与椭圆相切.
与椭圆相切.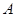 、
、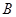 两点,求△
两点,求△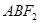 的面积
的面积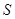 的最大值,并求此时直线的方程。
的最大值,并求此时直线的方程。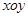 中,椭圆
中,椭圆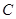 的标准方程为
的标准方程为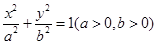 ,右焦点为
,右焦点为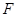 ,右准线为
,右准线为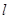 ,短轴的一个端点
,短轴的一个端点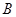 . 设原点到直线
. 设原点到直线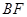 的距离为
的距离为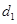 ,
,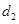 . 若
. 若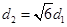 ,则椭圆
,则椭圆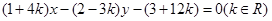 所经过的定点
所经过的定点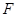 恰好是椭圆
恰好是椭圆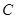 的一个焦点,且椭圆
的一个焦点,且椭圆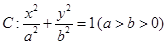 .
.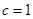 ,且
,且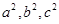 成等差数列,求椭圆
成等差数列,求椭圆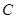 的方程;
的方程;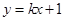 相交于
相交于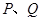 两点,求
两点,求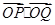 的取值范围.
的取值范围.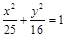 的左、右焦点,P为椭圆上任一点,点M的坐标为(6,4),则
的左、右焦点,P为椭圆上任一点,点M的坐标为(6,4),则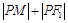 的最大值为__________.
的最大值为__________.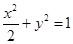 的左焦点
的左焦点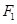 作直线
作直线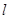 交椭圆于
交椭圆于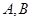 两点,
两点,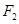 是椭圆右焦点,则
是椭圆右焦点,则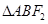 的周长为( )
的周长为( )
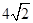


 过点
过点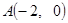 ,且与圆
,且与圆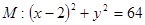 相内切,则动圆
相内切,则动圆