题目内容
设 ,用
,用 表示
表示 当
当 时的函数值中整数值的个数.
时的函数值中整数值的个数.
(1)求 的表达式.
的表达式.
(2)设 ,求
,求 .
.
(3)设 ,若
,若 ,求
,求 的最小值.
的最小值.
 ,用
,用 表示
表示 当
当 时的函数值中整数值的个数.
时的函数值中整数值的个数.(1)求
 的表达式.
的表达式.(2)设
 ,求
,求 .
.(3)设
 ,若
,若 ,求
,求 的最小值.
的最小值.(1) ;(2)
;(2) ;(3)
;(3) 的最小值是7.
的最小值是7.
 ;(2)
;(2) ;(3)
;(3) 的最小值是7.
的最小值是7.试题分析:(1)求出函数
 在
在 上的值域,根据值域即可确定其中的整数值的个数,从而得函数
上的值域,根据值域即可确定其中的整数值的个数,从而得函数 的表达式.(2)由(1)可得
的表达式.(2)由(1)可得 .为了求
.为了求 ,可将相邻两项结合,看作一项,这样便可转化为一个等差数列的求和问题,从而用等差数列的求和公式解决. (3)易得
,可将相邻两项结合,看作一项,这样便可转化为一个等差数列的求和问题,从而用等差数列的求和公式解决. (3)易得 .由等差数列与等比数列的积或商构成的新数列,求和时用错位相消法.
.由等差数列与等比数列的积或商构成的新数列,求和时用错位相消法. ,则
,则 大于等于
大于等于 的上限值.
的上限值.试题解析:对
 ,函数
,函数 在
在 单增,值域为
单增,值域为 , 故
, 故 .
.(2)
 ,故
,故


 .
.(3)由
 得
得 ,且
,且
两式相减,得


于是
 故若
故若 且
且 ,则
,则 的最小值是7.
的最小值是7.
练习册系列答案
相关题目
 满足
满足 (
( 为常数,
为常数, )
) 时,求
时,求 ;
; 时,求
时,求 的值;
的值; 恒成立的常数
恒成立的常数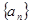 中,
中,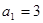 ,前n项和为
,前n项和为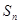
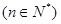 ,当
,当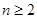 时,有
时,有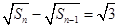 .(1)求数列
.(1)求数列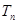 是数列
是数列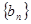 的前
的前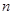 项和,若
项和,若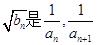 的等比中项,求
的等比中项,求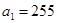 ,
,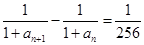
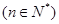 ,
,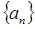 的通项公式
的通项公式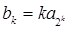 (
(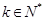 ),记数列
),记数列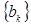 的前k项和为
的前k项和为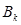 ,求
,求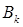 的最大值.
的最大值. ,则
,则 .
. 行的第2个数是 .
行的第2个数是 .
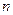 项和,若a1,a2,a5成等比数列,则S8="(" )
项和,若a1,a2,a5成等比数列,则S8="(" ) ,在验证n=1成立时,等式左边是
,在验证n=1成立时,等式左边是 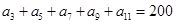 ,则
,则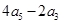 的值为( )
的值为( )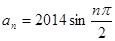 ,则
,则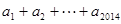 =( )
=( )