题目内容
(本题满分14分)如图,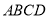 是边长为
是边长为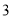 的正方形,
的正方形,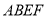 是矩形,平面
是矩形,平面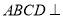 平面
平面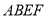 ,
,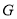 为
为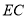 的中点.
的中点.

(1)求证: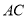 //平面
//平面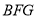 ;
;
(2)若三棱锥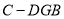 的体积为
的体积为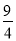 ,求三棱柱
,求三棱柱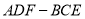 的体积.
的体积.
(1)见解析;(2)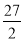
【解析】
试题解析:(1)连接 AE,设BF∩AE=O,连接OG,
∵四边形形 ABEF 是矩形,∴O为 AE的中点,
∵G 为EC的中点 ,∴OG 为△OAC 的中位线,
∴AC //OG 2分
∵OG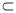 平面BFG, AC
平面BFG, AC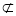 平面BFG
平面BFG
∴AC //平面BFG 4分
(2)平面ABCD⊥平面ABEF,ABEF 是矩形,
∴BE⊥AB ,又平面ABCD∩平面ABEF=AB,
∴BE⊥面ABCD,同理可得BC⊥面ABEF 7 分
∵BC∩BE=B,∴AB⊥面BCE ,则三棱柱 AFD-BEC 是直三棱柱,
∴ DC⊥面BEC, DC 平面DCEF,
平面DCEF,
∴平面DCEF⊥平面BEC,又平面DCEF∩平面BEC=EC,
作BH⊥EC,垂足为H,则BH⊥平面DCEF, 9 分
设BE=a,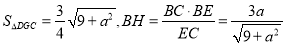 ,
,
∴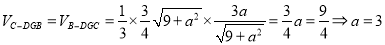 11分
11分
由上证可知,三棱柱AFD-BEC是直三棱柱,AB是其高,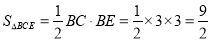 ,
,
所以,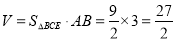 14 分
14 分
考点: 考查了直线与平面平行的判定,

练习册系列答案
相关题目
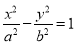 的焦点到其渐近线的距离等于2,抛物线
的焦点到其渐近线的距离等于2,抛物线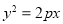 的焦点为双曲线的右焦点,双曲线截抛物线的准线所得的线段长为4,则抛物线方程为
的焦点为双曲线的右焦点,双曲线截抛物线的准线所得的线段长为4,则抛物线方程为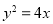 B.
B.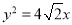 C.
C.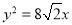 D.
D.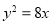
 则
则 的值为
的值为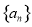 满足
满足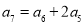 ,若存在不同的两项
,若存在不同的两项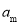 和
和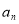 ,使得
,使得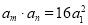 ,则
,则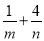 的最小值是__________.
的最小值是__________.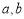 ,两个平面
,两个平面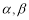 .给出下面四个命题:( )
.给出下面四个命题:( )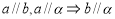 ;
; 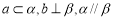
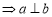 ;
;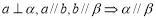 ;
; 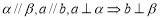 .
. 展开式中的常数项为________________(具体数字作答).
展开式中的常数项为________________(具体数字作答).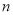 的值为
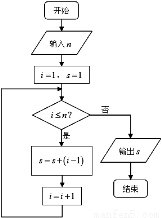
的值为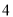 ,则输出
,则输出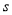 的值为____________.
的值为____________.