题目内容
若{ 、
、 、
、 }为空间的一组基底,则下列各项中,能构成基底的一组向量是
}为空间的一组基底,则下列各项中,能构成基底的一组向量是
- A.
 ,
, +
+ ,
, -
-
- B.
 ,
, +
+ ,
, -
-
- C.
 ,
, +
+ ,
, -
-
- D.
 +
+ ,
, -
- ,
, +2
+2
C
分析:空间的一组基底,必须是不共面的三个向量,利用向量共面的充要条件可证明A、B、D三个选项中的向量均为共面向量,利用反证法可证明C中的向量不共面
解答:∵( +
+ )+(
)+( -
- )=2
)=2 ,∴
,∴ ,
, +
+ ,
, -
- 共面,不能构成基底,排除 A;
共面,不能构成基底,排除 A;
∵( +
+ )-(
)-( -
- )=2
)=2 ,∴
,∴ ,
, +
+ ,
, -
- 共面,不能构成基底,排除 B;
共面,不能构成基底,排除 B;
∵ +2
+2 =
= (
( +
+ )-
)- (
( -
- ),∴,
),∴, +
+ ,
, -
- ,
, +2
+2 共面,不能构成基底,排除 D;
共面,不能构成基底,排除 D;
若 、
、 +
+ 、
、 -
- 共面,则
共面,则 =λ(
=λ( +
+ )+m(
)+m( -
- )=(λ+m)
)=(λ+m) +(λ-m)
+(λ-m) ,则
,则 、
、 、
、 为共面向量,此与{
为共面向量,此与{ 、
、 、
、 }为空间的一组基底矛盾,故
}为空间的一组基底矛盾,故 ,
, +
+ ,
, -
- 可构成空间向量的一组基底.
可构成空间向量的一组基底.
故选:C
点评:本题主要考查了空间向量基本定理,向量共面的充要条件等基础知识,判断向量是否共面是解决本题的关键,属基础题
分析:空间的一组基底,必须是不共面的三个向量,利用向量共面的充要条件可证明A、B、D三个选项中的向量均为共面向量,利用反证法可证明C中的向量不共面
解答:∵(
 +
+ )+(
)+( -
- )=2
)=2 ,∴
,∴ ,
, +
+ ,
, -
- 共面,不能构成基底,排除 A;
共面,不能构成基底,排除 A;∵(
 +
+ )-(
)-( -
- )=2
)=2 ,∴
,∴ ,
, +
+ ,
, -
- 共面,不能构成基底,排除 B;
共面,不能构成基底,排除 B;∵
 +2
+2 =
= (
( +
+ )-
)- (
( -
- ),∴,
),∴, +
+ ,
, -
- ,
, +2
+2 共面,不能构成基底,排除 D;
共面,不能构成基底,排除 D;若
 、
、 +
+ 、
、 -
- 共面,则
共面,则 =λ(
=λ( +
+ )+m(
)+m( -
- )=(λ+m)
)=(λ+m) +(λ-m)
+(λ-m) ,则
,则 、
、 、
、 为共面向量,此与{
为共面向量,此与{ 、
、 、
、 }为空间的一组基底矛盾,故
}为空间的一组基底矛盾,故 ,
, +
+ ,
, -
- 可构成空间向量的一组基底.
可构成空间向量的一组基底.故选:C
点评:本题主要考查了空间向量基本定理,向量共面的充要条件等基础知识,判断向量是否共面是解决本题的关键,属基础题

练习册系列答案
相关题目
 、
、 、
、 }为空间的一组基底,则下列各项中,能构成基底的一组向量是( )
}为空间的一组基底,则下列各项中,能构成基底的一组向量是( ) ,
, +
+ ,
, -
-
 ,
, +
+ ,
, -
-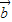
 ,
, +
+ ,
, -
-
 +
+ ,
, -
-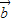 ,
, +2
+2